Comme application des notions de ce chapitre, nous proposons d'étudier
l'ensemble des solutions de l'équation de récurrence suivante :
où 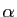 et
et 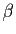 sont deux réels fixés.
L'exemple le plus simple
est l'équation définissant les nombres de Fibonacci,
sont deux réels fixés.
L'exemple le plus simple
est l'équation définissant les nombres de Fibonacci,
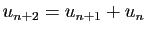 . Nous notons
. Nous notons  l'ensemble des suites de
réels qui vérifient
l'ensemble des suites de
réels qui vérifient
 . Dire que
. Dire que
 est linéaire revient à dire que
est linéaire revient à dire que  est un espace vectoriel.
est un espace vectoriel.
Proposition 12
L'ensemble  des suites de réels vérifiant
des suites de réels vérifiant
 est un espace
vectoriel de dimension
est un espace
vectoriel de dimension 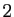 .
.
Démonstration : Commençons par vérifier que  est un sous-espace vectoriel de
l'ensemble des suites de réels. Nous en donnerons ensuite une base.
est un sous-espace vectoriel de
l'ensemble des suites de réels. Nous en donnerons ensuite une base.
Soient 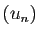 et
et 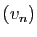 deux suites vérifiant
deux suites vérifiant
 ,
,
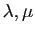 deux réels.
deux réels.
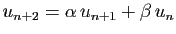
et
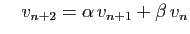
impliquent :
Donc
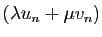 vérifie
vérifie
 . D'où le résultat en
appliquant le théorème 2. On peut aussi démontrer que
l'application qui à une suite
. D'où le résultat en
appliquant le théorème 2. On peut aussi démontrer que
l'application qui à une suite 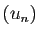 quelconque associe la suite de
terme général
quelconque associe la suite de
terme général
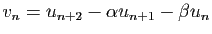 est une
application linéaire. L'ensemble
est une
application linéaire. L'ensemble  est le noyau de cette
aplication. C'est donc un sous-espace vectoriel de
est le noyau de cette
aplication. C'est donc un sous-espace vectoriel de
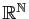 , par le théorème 6.
Considérons maintenant les deux suites
, par le théorème 6.
Considérons maintenant les deux suites 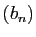 et
et 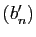 ,
vérifiant
,
vérifiant
 et telles que
et telles que
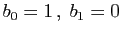
et
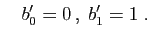
Soit 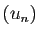 une suite quelconque vérifiant
une suite quelconque vérifiant
 . La suite
. La suite 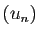 est définie de façon unique par la donnée de
est définie de façon unique par la donnée de
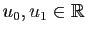 et l'équation
et l'équation
 . Donc la suite
. Donc la suite 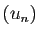 est égale à la
combinaison linéaire
est égale à la
combinaison linéaire
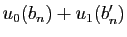 : la famille
: la famille
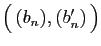 est génératrice. Supposons que
est génératrice. Supposons que 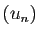 soit la suite
nulle. Alors
soit la suite
nulle. Alors 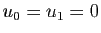 . Donc la famille
. Donc la famille
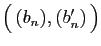 est libre : c'est une base.
est libre : c'est une base. 
Pour trouver une expression explicite aux solutions de
 , nous
allons trouver une autre base.
Nous commençons par écarter le cas où
, nous
allons trouver une autre base.
Nous commençons par écarter le cas où
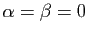 : dans
ce cas, les suites solutions de
: dans
ce cas, les suites solutions de
 sont nulles à partir du rang
2. Nous supposons désormais que
sont nulles à partir du rang
2. Nous supposons désormais que 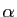 et
et 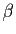 ne sont pas tous
les deux nuls. Cherchons quelles
suites géométriques vérifient
ne sont pas tous
les deux nuls. Cherchons quelles
suites géométriques vérifient
 . Supposons que
. Supposons que 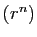 vérifie
vérifie
 . Alors,
. Alors,
C'est vrai si 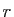 est nul, ou bien s'il est solution de l'équation du
second degré suivante, qu'on appelle l'équation caractéristique associée.
est nul, ou bien s'il est solution de l'équation du
second degré suivante, qu'on appelle l'équation caractéristique associée.
Démonstration : Puisque l'espace vectoriel  est de dimension
est de dimension 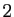 , il suffit dans
chacun des trois cas de montrer que les deux suites proposées
vérifient
, il suffit dans
chacun des trois cas de montrer que les deux suites proposées
vérifient
 et
forment une famille libre.
et
forment une famille libre.
Dans le premier cas, les deux suites
vérifient
 car
car 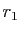 et
et 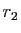 sont racines de
sont racines de 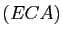 .
Pour montrer qu'elles forment une famille libre, supposons que la suite
.
Pour montrer qu'elles forment une famille libre, supposons que la suite
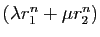 soit nulle. Les deux premiers termes
sont :
soit nulle. Les deux premiers termes
sont :
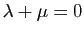
et
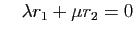
Puisque
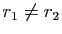 , ce système de deux équations a
une solution unique,
, ce système de deux équations a
une solution unique,
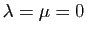 .
.
Dans le second cas la racine double est
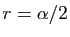 et elle est non
nulle, le cas
et elle est non
nulle, le cas
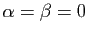 étant écarté.
Il est évident que
étant écarté.
Il est évident que 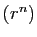 vérifie
vérifie
 . On le vérifie facilement pour
. On le vérifie facilement pour 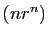 . Pour
montrer que la famille est libre, supposons que la suite
. Pour
montrer que la famille est libre, supposons que la suite
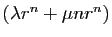 soit nulle. Les deux premiers termes sont :
soit nulle. Les deux premiers termes sont :
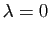
et
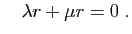
Donc (puisque 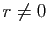 ),
),
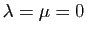 .
.
Traitons maintenant le dernier cas : 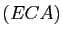 a deux racines complexes
conjuguées
a deux racines complexes
conjuguées
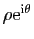 et
et
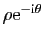 . Les suites (complexes)
. Les suites (complexes)
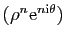 et
et
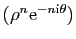 vérifient
vérifient
 .
Leur somme et leur différence
sont :
.
Leur somme et leur différence
sont :
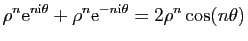
et
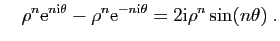
On en déduit que les deux suites proposées vérifient
 .
Pour montrer que la famille est libre, supposons que la suite
.
Pour montrer que la famille est libre, supposons que la suite
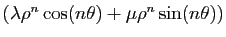 soit nulle. Les deux premiers termes sont :
soit nulle. Les deux premiers termes sont :
On en déduit donc que
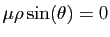 , donc
, donc 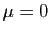 car
car
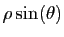 est non nul (sinon les racines de
est non nul (sinon les racines de 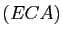 seraient
réelles).
seraient
réelles).
Comme premier exemple, considérons l'équation définissant les
nombres de Fibonacci :
L'équation caractéristique associée
est
Elle a deux racines réelles distinctes, 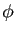 et
et 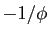 , où
, où
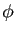 est le nombre d'or :
est le nombre d'or :
L'ensemble des suites réelles vérifiant
 est donc
est donc
Les nombres de Fibonacci sont définis par
 , avec
, avec 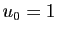 et
et
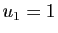 . Pour calculer les coordonnées
. Pour calculer les coordonnées 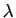 et
et 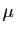 de cette
suite, il faut résoudre le système
de cette
suite, il faut résoudre le système
On en déduit l'expression suivante du 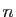 -ième nombre de Fibonacci :
-ième nombre de Fibonacci :
(Persuadez-vous que 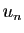 est bien un entier !)
Considérons maintenant l'équation suivante.
est bien un entier !)
Considérons maintenant l'équation suivante.
L'équation caractéristique associée est :
Ses racines sont :
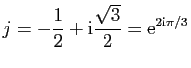
et
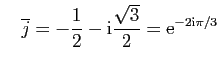
Toute solution réelle de l'équation de récurrence s'écrit :
Les solutions sont périodiques de période 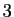 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() et
et ![]() deux suites vérifiant
deux suites vérifiant
![]() ,
,
![]() deux réels.
deux réels.
![]() , nous
allons trouver une autre base.
Nous commençons par écarter le cas où
, nous
allons trouver une autre base.
Nous commençons par écarter le cas où
![]() : dans
ce cas, les suites solutions de
: dans
ce cas, les suites solutions de
![]() sont nulles à partir du rang
2. Nous supposons désormais que
sont nulles à partir du rang
2. Nous supposons désormais que ![]() et
et ![]() ne sont pas tous
les deux nuls. Cherchons quelles
suites géométriques vérifient
ne sont pas tous
les deux nuls. Cherchons quelles
suites géométriques vérifient
![]() . Supposons que
. Supposons que ![]() vérifie
vérifie
![]() . Alors,
. Alors,
![]() car
car ![]() et
et ![]() sont racines de
sont racines de ![]() .
Pour montrer qu'elles forment une famille libre, supposons que la suite
.
Pour montrer qu'elles forment une famille libre, supposons que la suite
![]() soit nulle. Les deux premiers termes
sont :
soit nulle. Les deux premiers termes
sont :
![]() et elle est non
nulle, le cas
et elle est non
nulle, le cas
![]() étant écarté.
Il est évident que
étant écarté.
Il est évident que ![]() vérifie
vérifie
![]() . On le vérifie facilement pour
. On le vérifie facilement pour ![]() . Pour
montrer que la famille est libre, supposons que la suite
. Pour
montrer que la famille est libre, supposons que la suite
![]() soit nulle. Les deux premiers termes sont :
soit nulle. Les deux premiers termes sont :
![]() a deux racines complexes
conjuguées
a deux racines complexes
conjuguées
![]() et
et
![]() . Les suites (complexes)
. Les suites (complexes)
![]() et
et
![]() vérifient
vérifient
![]() .
Leur somme et leur différence
sont :
.
Leur somme et leur différence
sont :
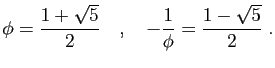
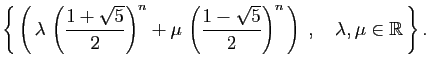
![\begin{displaymath}
\left\{
\begin{array}{lcl}
\lambda+\mu&=&1 [1.5ex]
\lambda\phi-\mu/\phi&=&1
\end{array}\right.
\end{displaymath}](img456.gif)
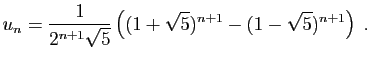
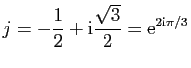 et
et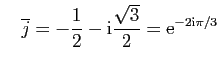
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales