Toute équation différentielle peut se ramener à une
équation d'ordre ![]() , homogène en temps, quitte à accepter une
augmentation de la dimension. De plus pour une telle
équation, on peut toujours ramener l'origine du temps en 0. Il est donc
naturel de considérer le problème différentiel avec condition
initiale suivant, dit «problème de Cauchy» :
, homogène en temps, quitte à accepter une
augmentation de la dimension. De plus pour une telle
équation, on peut toujours ramener l'origine du temps en 0. Il est donc
naturel de considérer le problème différentiel avec condition
initiale suivant, dit «problème de Cauchy» :
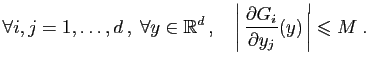
Pour montrer que le problème de Cauchy (10) admet une
solution unique définie sur tout
![]() , il suffit de montrer que
pour tout
, il suffit de montrer que
pour tout ![]() , il admet une solution unique définie sur
, il admet une solution unique définie sur ![]() .
Considérons l'espace des fonctions continues de
.
Considérons l'espace des fonctions continues de ![]() dans
dans
![]() ,
,
![]() .
C'est un espace vectoriel normé complet (espace de Banach).
Définissons dans cet espace l'opérateur
.
C'est un espace vectoriel normé complet (espace de Banach).
Définissons dans cet espace l'opérateur ![]() qui à une fonction
continue
qui à une fonction
continue ![]() associe la fonction
associe la fonction ![]() définie par :
définie par :
![$\displaystyle \forall t\in [0,T]\;,\quad \Phi(z)(t) = y_0 +
\int_{0}^t G(z(s)) \mathrm{d}s\;.
$](img762.gif)
![]() On pourrait penser au vu de ce qui précède que
calculer la suite des itérés
On pourrait penser au vu de ce qui précède que
calculer la suite des itérés
![]() constitue
une méthode de calcul approché de la solution
constitue
une méthode de calcul approché de la solution ![]() . Malheureusement, le
calcul de
. Malheureusement, le
calcul de
![]() implique le calcul de
implique le calcul de ![]() intégrales
successives, entraînant des erreurs d'approximations qui se cumulent.
Cette méthode n'est donc pas utilisée en pratique.
intégrales
successives, entraînant des erreurs d'approximations qui se cumulent.
Cette méthode n'est donc pas utilisée en pratique.
Exemple : Explicitons le calcul des itérés
![]() dans un cas particulier :
dans un cas particulier :
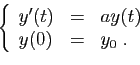
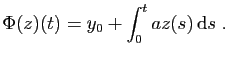
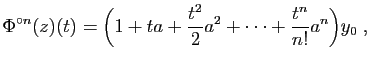
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales