Il peut sembler paradoxal de modéliser l'évolution dans le temps
de la taille d'une population, qui est un nombre entier d'individus, par
la solution d'une équation différentielle, qui est nécessairement
une fonction continue (et même dérivable). Une population animale
évolue par les naissances et les décès, qui la font augmenter ou
diminuer chaque fois d'une unité. Mais pour une population de grande taille,
et selon l'échelle de temps à laquelle on se place, les variations de la
population pourront effectivement apparaître comme continues. Concernant
la population humaine sur la terre, de l'ordre de 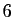 milliards individus,
les nombres de naissances et de décès qui ont lieu chaque
seconde sont de plusieurs milliers. Ces nombres, même s'ils ne sont pas
définis très rigoureusement, sont compris par chacun comme des moyennes
sur les secondes contenues dans un intervalle de temps suffisant. Il y a
milliards individus,
les nombres de naissances et de décès qui ont lieu chaque
seconde sont de plusieurs milliers. Ces nombres, même s'ils ne sont pas
définis très rigoureusement, sont compris par chacun comme des moyennes
sur les secondes contenues dans un intervalle de temps suffisant. Il y a
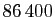 secondes dans un jour,
secondes dans un jour,
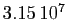 dans une année. Il est assez
raisonnable de penser que les nombres d'individus naissant le 7
décembre 2006 et le 8 décembre 2006, sont assez proches. Parler du nombre
d'individus naissant par seconde le 8 décembre 2006 suppose qu'on ne
distinguera pas si la seconde a lieu entre 8h et 9h ou entre 16h et 17h. Il
est d'ailleurs impossible de connaître toutes les dates de naissance à
la seconde près. Le seul sens
que l'on puisse donner à la phrase «la population de la
terre a augmenté de 30 individus par seconde le 8 décembre 2006» est :
«la population de la terre a augmenté
de
dans une année. Il est assez
raisonnable de penser que les nombres d'individus naissant le 7
décembre 2006 et le 8 décembre 2006, sont assez proches. Parler du nombre
d'individus naissant par seconde le 8 décembre 2006 suppose qu'on ne
distinguera pas si la seconde a lieu entre 8h et 9h ou entre 16h et 17h. Il
est d'ailleurs impossible de connaître toutes les dates de naissance à
la seconde près. Le seul sens
que l'on puisse donner à la phrase «la population de la
terre a augmenté de 30 individus par seconde le 8 décembre 2006» est :
«la population de la terre a augmenté
de 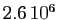 individus ce jour là,
ce qui fait une moyenne de 30 par seconde environ». Mais alors, il faudra
bien considérer que dans un intervalle de 2 secondes l'augmentation est
de 60, dans un intervalle de 3 secondes 90, etc.
Notons
individus ce jour là,
ce qui fait une moyenne de 30 par seconde environ». Mais alors, il faudra
bien considérer que dans un intervalle de 2 secondes l'augmentation est
de 60, dans un intervalle de 3 secondes 90, etc.
Notons 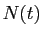 la population de la terre à l'instant
la population de la terre à l'instant 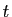 , et choisissons la
seconde comme unité de temps. Nous venons
de dire que l'accroissement de population dans un intervalle de
temps de
, et choisissons la
seconde comme unité de temps. Nous venons
de dire que l'accroissement de population dans un intervalle de
temps de 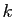 secondes,
secondes,
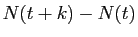 vaut
vaut
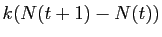 .
Cela revient bien à considérer le rapport
.
Cela revient bien à considérer le rapport
comme constant pour de petites valeurs de 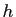 . Ce rapport est
appelé taux de variation de la population. Lui affecter une valeur
donnée, c'est modéliser
. Ce rapport est
appelé taux de variation de la population. Lui affecter une valeur
donnée, c'est modéliser 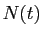 comme une fonction dérivable du temps,
et le taux de variation est alors la valeur de la dérivée
comme une fonction dérivable du temps,
et le taux de variation est alors la valeur de la dérivée 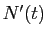 .
De même, on parlera de taux de naissance et de taux de décès
pour les nombres moyens de naissances et de décès par unité de temps,
même si on reste conscient du fait qu'il ne s'agit que de moyennes
approximatives.
.
De même, on parlera de taux de naissance et de taux de décès
pour les nombres moyens de naissances et de décès par unité de temps,
même si on reste conscient du fait qu'il ne s'agit que de moyennes
approximatives.
Ce qui précède n'a de valeur que pour modéliser l'évolution de la
population à une échelle de temps bien supérieure à la seconde.
Plus qu'au nombre exact de naissances ou de décès par seconde, on
s'intéresse, pour des raisons de planification économique par exemple,
à l'évolution de la population sur les 10 années qui viennent. Il est
clair que le taux de variation de la population, s'il vaut 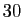 par seconde
le 8 décembre 2006, pourra changer au cours des dix ans qui viennent, en
fonction des ressources naturelles, de la taille de la population elle-même,
ou d'autres facteurs, comme la température moyenne de
l'atmosphère.
par seconde
le 8 décembre 2006, pourra changer au cours des dix ans qui viennent, en
fonction des ressources naturelles, de la taille de la population elle-même,
ou d'autres facteurs, comme la température moyenne de
l'atmosphère.
Le modèle différentiel le plus simple, dit «modèle de Malthus»,
consiste à écrire que les taux de naissance et de décès
sont proportionnels à la taille de la population. Il peut sembler
évident que plus la population est importante, plus il naît et meurt
d'individus par seconde. On introduit
les notions de taux de fertilité (nombre de naissances par
unité de temps et par individu) et de taux de mortalité (nombre
de décès par unité de temps et par individu), que l'on suppose
constants. Ils sont notés 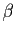 et
et 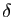 respectivement. Le taux de
variation est alors la différence :
respectivement. Le taux de
variation est alors la différence :
La solution de cette équation, partant de la population 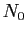 à l'instant
0 est :
à l'instant
0 est :
Figure 9:
Modèle de Malthus.
|
|
Si la fertilité l'emporte sur la mortalité (
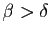 ), le modèle
de Malthus prévoit une croissance «exponentielle»
de la population. Dans
le cas
), le modèle
de Malthus prévoit une croissance «exponentielle»
de la population. Dans
le cas
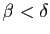 , la population doit décroître jusqu'à son
extinction. En
fait le modèle de Malthus, s'il peut convenir pour des populations isolées
de bactéries sur un intervalle de temps court, est beaucoup trop
simpliste pour rendre compte de populations interagissant avec leur milieu,
comme la nôtre.
, la population doit décroître jusqu'à son
extinction. En
fait le modèle de Malthus, s'il peut convenir pour des populations isolées
de bactéries sur un intervalle de temps court, est beaucoup trop
simpliste pour rendre compte de populations interagissant avec leur milieu,
comme la nôtre.
Ceci a été reconnu très tôt et d'autres modèles différentiels
ont introduit
des sophistications supplémentaires dans le calcul du taux
de variation. Le modèle de Verhulst, ou modèle de croissance
logistique, considère que le taux de variation, s'il peut être en gros
proportionnel à la taille pour de petites populations, atteindra une
valeur maximale pour une certaine taille, puis décroîtra
pour s'annuler quand la population atteint une taille critique 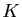 ,
interprétée comme le nombre maximum d'individus que l'environnement peut
supporter. Ceci correspond à l'équation :
,
interprétée comme le nombre maximum d'individus que l'environnement peut
supporter. Ceci correspond à l'équation :
Ce modèle prévoit que la population augmente et converge vers
sa taille critique (cf. figure 10).
Plus précisément :
Figure 10:
Modèle de Verhulst.
|
|
De nombreux autres modèles ont été proposés, sous forme d'équations
du type :
Dans une étude menée au Canada en 1978 sur les vers du bourgeon de
l'épicéa, le modèle était le suivant :
Par rapport au modèle de Verhulst, le nouveau terme modélise
l'action d'un prédateur sur la population. Si 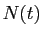 est faible,
le prédateur a peu d'influence sur la croissance. La prédation augmente
avec la population, devient significative quand
est faible,
le prédateur a peu d'influence sur la croissance. La prédation augmente
avec la population, devient significative quand 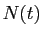 est de l'ordre de
est de l'ordre de 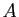 ,
pour atteindre rapidement ensuite sa valeur maximale.
Les 4 paramètres du modèle sont
,
pour atteindre rapidement ensuite sa valeur maximale.
Les 4 paramètres du modèle sont 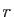 (le taux de fertilité
sans prédateur),
(le taux de fertilité
sans prédateur), 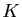 (la population maximale supportée par
l'environnement sans prédateur),
(la population maximale supportée par
l'environnement sans prédateur), 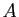 (le seuil de déclenchement
de la prédation) et
(le seuil de déclenchement
de la prédation) et  (qui contrôle l'intensité maximale
de prédation). Supposons que le temps soit exprimé en secondes (
(qui contrôle l'intensité maximale
de prédation). Supposons que le temps soit exprimé en secondes (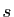 ), et
les nombres d'individus en milliers (
), et
les nombres d'individus en milliers (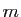 ). Alors
). Alors 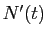 est
mesuré en
est
mesuré en 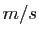 ,
, 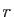 est en
est en 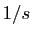 ,
, 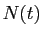 ,
, 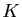 et
et 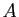 sont mesurés
en
sont mesurés
en 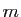 et
et  en
en 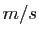 . Changer d'unité pour compter
la population (par exemple passer du millier à la dizaine de milliers),
revient à multiplier
. Changer d'unité pour compter
la population (par exemple passer du millier à la dizaine de milliers),
revient à multiplier 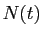 par une constante. De même, changer
l'unité de temps (en passant par exemple de la seconde à la minute),
revient à multiplier le taux de variation par une autre constante.
Or ces changements d'unités ne peuvent pas modifier le comportement
qualitatif du modèle. Pour simplifier l'étude, on est amené à
effectuer des changements de variables, qui permettent à la fois de
diminuer le nombre des paramètres et de donner une forme plus compacte à
l'équation. Par exemple, dans le modèle ci-dessus, posons :
par une constante. De même, changer
l'unité de temps (en passant par exemple de la seconde à la minute),
revient à multiplier le taux de variation par une autre constante.
Or ces changements d'unités ne peuvent pas modifier le comportement
qualitatif du modèle. Pour simplifier l'étude, on est amené à
effectuer des changements de variables, qui permettent à la fois de
diminuer le nombre des paramètres et de donner une forme plus compacte à
l'équation. Par exemple, dans le modèle ci-dessus, posons :
Remarquons que les nouvelles quantités sont des nombres réels sans
unité. Le modèle devient :
Cette équation ne contient plus que deux paramètres, 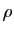 et
et 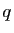 .
Transformer les variables d'un modèle pour se ramener à des variables
sans unités se dit «dédimensionner».
.
Transformer les variables d'un modèle pour se ramener à des variables
sans unités se dit «dédimensionner».
Pour aller plus loin dans l'étude de l'influence de la prédation sur
une population, il faut inclure dans l'étude la population des
prédateurs. Le modèle de Lotka-Volterra est le premier qui en ait tenu
compte. Notons 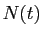 le nombre de proies à l'instant
le nombre de proies à l'instant 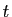 , et
, et 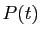 le
nombre de prédateurs. Le modèle s'écrit :
le
nombre de prédateurs. Le modèle s'écrit :
Dans les deux taux de variation apparaissent 4 termes, supposés positifs,
dont l'interprétation est la suivante :
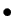
-
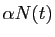 est le taux d'accroissement de la population, en l'absence
de prédateur.
est le taux d'accroissement de la population, en l'absence
de prédateur.
-
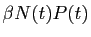 est le taux de prélèvement des proies par les
prédateurs.
est le taux de prélèvement des proies par les
prédateurs.
-
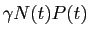 est le taux d'accroissement de la population des
prédateurs, quand
est le taux d'accroissement de la population des
prédateurs, quand 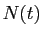 proies sont disponibles.
proies sont disponibles.
-
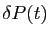 est le taux de diminution de la population des prédateurs
quand aucune proie n'est disponible.
est le taux de diminution de la population des prédateurs
quand aucune proie n'est disponible.
Les évolutions de 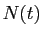 et
et 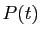 prévues par le modèle sont
périodiques (figure 11).
prévues par le modèle sont
périodiques (figure 11).
Figure 11:
Modèle de Lotka-Volterra.
|
|
Partant d'une situation où les proies sont nombreuses
et les prédateurs rares, la population des prédateurs va rapidement
augmenter, grâce à l'abondance des ressources. Les prédateurs devenus
nombreux, la population des proies déclinera rapidement. Ce déclin
entraînera ensuite celui des prédateurs. Les prédateurs redevenus
rares, la population des proies pourra augmenter à nouveau.
Les généralisations de ce modèle permettent de
modéliser plus de deux populations, ou d'inclure d'autres
types d'interactions.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
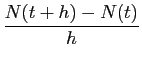
![]() par seconde
le 8 décembre 2006, pourra changer au cours des dix ans qui viennent, en
fonction des ressources naturelles, de la taille de la population elle-même,
ou d'autres facteurs, comme la température moyenne de
l'atmosphère.
par seconde
le 8 décembre 2006, pourra changer au cours des dix ans qui viennent, en
fonction des ressources naturelles, de la taille de la population elle-même,
ou d'autres facteurs, comme la température moyenne de
l'atmosphère.
![]() et
et ![]() respectivement. Le taux de
variation est alors la différence :
respectivement. Le taux de
variation est alors la différence :
![]() ,
interprétée comme le nombre maximum d'individus que l'environnement peut
supporter. Ceci correspond à l'équation :
,
interprétée comme le nombre maximum d'individus que l'environnement peut
supporter. Ceci correspond à l'équation :
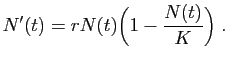
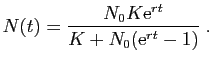
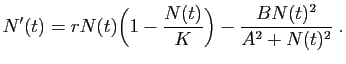
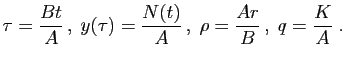
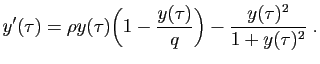
![]() le nombre de proies à l'instant
le nombre de proies à l'instant ![]() , et
, et ![]() le
nombre de prédateurs. Le modèle s'écrit :
le
nombre de prédateurs. Le modèle s'écrit :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales