Il existe de très nombreuses méthodes numériques de résolution
des équations différentielles : plus ou moins précises, plus ou moins
coûteuses en temps de calcul, plus ou moins adaptées à tel ou tel type
d'équation. Toutes ces méthodes ont été implémentées et les
meilleures sont proposées dans les logiciels de calcul standard. Pour
comprendre la problématique de la résolution numérique, nous
détaillerons seulement la méthode la plus simple, qui est la
méthode d'Euler.
Nous nous plaçons dans le cadre du théorème de
Cauchy-Lipschitz. Le problème
à résoudre est le problème de Cauchy (10) :
Nous supposons que les hypothèses du théorème 7 sont
vérifiées : la fonction 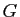 est continûment différentiable sur
est continûment différentiable sur
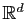 et ses dérivées partielles sont bornées. Notre problème
est de construire une approximation numérique de la solution. Il
faut pour cela discrétiser le temps. Nous choisissons donc un
pas de discrétisation
et ses dérivées partielles sont bornées. Notre problème
est de construire une approximation numérique de la solution. Il
faut pour cela discrétiser le temps. Nous choisissons donc un
pas de discrétisation 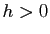 . Les multiples entiers de
. Les multiples entiers de 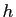 sont
les instants de discrétisation.
sont
les instants de discrétisation.
Remarque : Dans certains cas, il est judicieux d'adapter la suite des
instants de discrétisation aux valeurs de la solution : plus espacés
là où la solution varie peu, ils seront plus rapprochés là où
la solution varie rapidement. On parle dans ce cas de méthode à pas
adaptatif.
Notre but est de calculer par récurrence dans
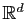 une suite de valeurs
une suite de valeurs
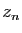 qui seront
comprises comme des approximations de la fonction aux instants de
discrétisation. En ces instants, la solution exacte vérifie :
qui seront
comprises comme des approximations de la fonction aux instants de
discrétisation. En ces instants, la solution exacte vérifie :
Or si le pas 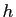 est petit, la valeur de l'intégrale est proche du produit
est petit, la valeur de l'intégrale est proche du produit
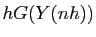 (la «surface du rectangle» en dimension
(la «surface du rectangle» en dimension 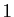 ). Il est naturel
de définir la suite
). Il est naturel
de définir la suite 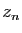 par
par 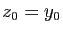 et pour tout
et pour tout
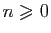 :
:
Exemple : Explicitons le calcul des vecteurs 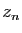 dans le
cas particulier d'un système linéaire à coefficients constants :
dans le
cas particulier d'un système linéaire à coefficients constants :
On a :
Avec la condition initiale 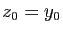 , on obtient :
, on obtient :
La fonction censée approcher 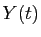 sera notée
sera notée 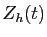 . Elle est
définie entre les instants de discrétisation par une interpolation
linéaire :
. Elle est
définie entre les instants de discrétisation par une interpolation
linéaire :
La majoration (11) montre que l'erreur commise en
remplaçant la solution exacte par la solution approchée est de l'ordre
de 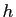 , et tend donc vers 0 quand
, et tend donc vers 0 quand 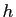 tend vers 0. La constante
multiplicative montre que l'erreur sur
tend vers 0. La constante
multiplicative montre que l'erreur sur ![$ [0,T]$](img758.gif) peut dépendre fortement de
peut dépendre fortement de
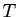 . On comprend intuitivement que, partant d'une condition initiale exacte,
les erreurs commises à chaque pas puissent se cumuler,
de sorte que l'erreur à l'instant
. On comprend intuitivement que, partant d'une condition initiale exacte,
les erreurs commises à chaque pas puissent se cumuler,
de sorte que l'erreur à l'instant 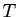 est exponentielle en
est exponentielle en 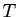 .
.
Exemple : Considérons le cas de l'exponentielle dans
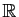 :
:
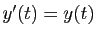 , avec
, avec 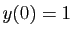 (figure 12).
(figure 12).
Figure 12:
Approximation de l'exponentielle par la méthode d'Euler.
|
|
La suite approximante est :
Pour 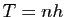 fixé, la valeur de
fixé, la valeur de 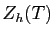 est :
est :
L'erreur commise est bien de l'ordre de 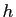 . Le tableau 1 donne
les valeurs de l'erreur
. Le tableau 1 donne
les valeurs de l'erreur
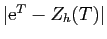 , pour
, pour 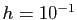 ,
, 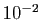 et
et
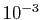 , et
, et 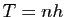 allant de
allant de 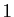 à
à 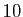 . Même pour
. Même pour 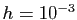 , on
constate que l'erreur en
, on
constate que l'erreur en 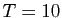 est très importante.
est très importante.
Tableau 1:
Erreurs de la méthode d'Euler sur
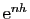 .
.
 |
La méthode d'Euler, très facile à programmer et peu coûteuse en temps
de calcul, peut suffire pour certaines applications. De nombreuses autres
méthodes ont été imaginées. Nous nous contenterons d'indiquer une
voie de généralisation.
L'idée de base de la méthode d'Euler était d'approcher :
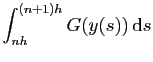
par
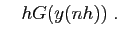
Ceci est l'approximation la plus rudimentaire (méthode des rectangles
à gauche) pour un calcul d'intégrale. On peut faire beaucoup mieux, par
exemple par la méthode des trapèzes. Il s'agit alors d'approcher
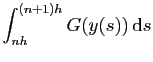
par
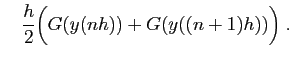
Ceci conduit à définir la suite des valeurs approchées 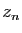 par
par
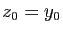 et pour tout
et pour tout
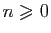 :
:
Sous cette forme, 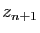 est définie comme la solution d'une équation,
qu'il faut résoudre numériquement. On dit
dans ce cas que la méthode est implicite. Pour la rendre explicite,
on peut remplacer dans le membre de droite
est définie comme la solution d'une équation,
qu'il faut résoudre numériquement. On dit
dans ce cas que la méthode est implicite. Pour la rendre explicite,
on peut remplacer dans le membre de droite 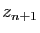 par l'approximation
issue de la méthode d'Euler. Cela donne :
par l'approximation
issue de la méthode d'Euler. Cela donne :
Ce que l'on obtient est un cas particulier de la méthode de Runge-Kutta.
Notons que les calculs seront nécessairement plus coûteux, car ils
demandent à chaque pas deux évaluations de la fonction 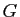 , au lieu d'une.
En revanche, on obtiendra un résultat plus précis : on démontre que
l'erreur commise sur un intervalle de temps fixé
, au lieu d'une.
En revanche, on obtiendra un résultat plus précis : on démontre que
l'erreur commise sur un intervalle de temps fixé ![$ [0,T]$](img758.gif) est de l'ordre
de
est de l'ordre
de 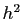 , contre
, contre 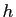 pour la méthode d'Euler.
pour la méthode d'Euler.
Exemple : Reprenons le cas de l'exponentielle dans
 :
:
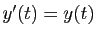 , avec
, avec 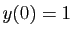 . La suite approximante est solution de
l'équation de récurrence :
. La suite approximante est solution de
l'équation de récurrence :
soit :
Le tableau 2 donne
les valeurs de l'erreur
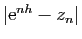 , pour
, pour 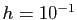 ,
, 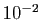 et
et
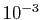 , et
, et 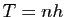 allant de
allant de 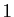 à
à 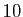 . On constate que les
erreurs sont beaucoup plus faibles que celles de la méthode d'Euler.
. On constate que les
erreurs sont beaucoup plus faibles que celles de la méthode d'Euler.
Tableau 2:
Erreurs de la méthode de Runge-Kutta sur
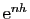 .
.
 |
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
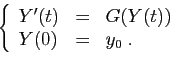
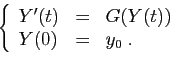
![]() une suite de valeurs
une suite de valeurs
![]() qui seront
comprises comme des approximations de la fonction aux instants de
discrétisation. En ces instants, la solution exacte vérifie :
qui seront
comprises comme des approximations de la fonction aux instants de
discrétisation. En ces instants, la solution exacte vérifie :
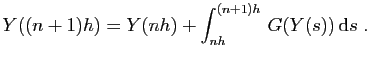
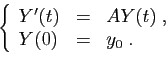
![]() sera notée
sera notée ![]() . Elle est
définie entre les instants de discrétisation par une interpolation
linéaire :
. Elle est
définie entre les instants de discrétisation par une interpolation
linéaire :
![]() :
:
![]() , avec
, avec ![]() (figure 12).
(figure 12).
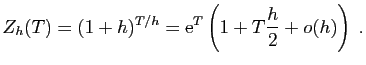
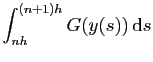 par
par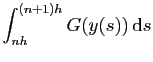 par
par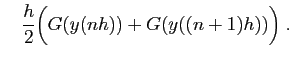
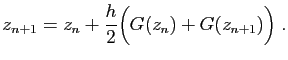
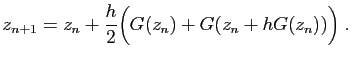
![]() :
:
![]() , avec
, avec ![]() . La suite approximante est solution de
l'équation de récurrence :
. La suite approximante est solution de
l'équation de récurrence :
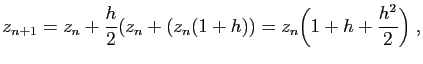
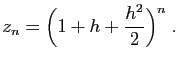
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales