sqrt(a^2-2*a*b+b^2) ne
retourne-t-elle pas a-b ? Par quelles commandes faut-il la
compléter pour obtenir a-b ?
sin(evalf(10^15*pi)) evalf(sin(10^15*pi))
f:=x^2. Expliquer pourquoi la commande
f(2) ne retourne pas 4. Que faudrait-il saisir pour obtenir 4 ?
size([a$10]) et size(%{a$10%}).
diff(x^2*y^2) et
diff(X^2*Y^2). Quelle commande retourne la liste
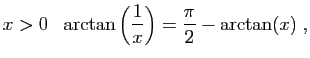
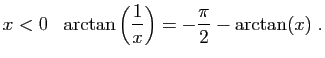
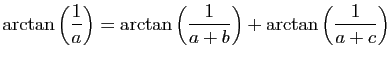
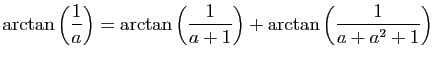

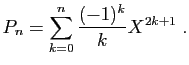
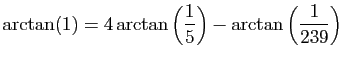
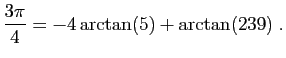
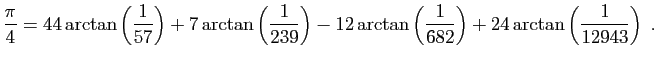
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales