-
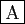
evalf(2^3/4)-
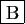
normal(2^3/4)-
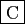
2^(3/4)-
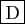
2^3/4;-
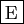
2^3/4.
evalf(2^3/4)
normal(2^3/4)
2^(3/4)
2^3/4;
2^3/4.
a n'a pas été affectée. La ligne de
commande proposée affiche la valeur exacte (2*a)/a
2*a/a
normal((a+a)/a)
logb(a^2,a)
expand((a+a)/a)
c.
c:=4/2
c=2/1
c==2
c:=sqrt(4)
c:=4/2.
a a été affectée à la valeur
exacte b.
b=a+a
b:=2.*a/a
b:=3*a-a
b:=a^2
b:=a^2+a
a n'a pas été affectée. La ligne de
commande proposée affiche la valeur exacte normal(sqrt(4*a^4)/a^2)
normal(sqrt(4*a^2)/a)
simplify(ln(a^2)/ln(a))
normal(ln(a^2)/ln(a))
simplify(sqrt(4*a^2/a)
f qui à
f:=sin
f:=sin(x)
f:=unapply(sin(x))
f(x):=sin(x)
f=x->sin(x)
sin(x)
x->sin(x)
diff(cos(x),x)
int(cos(x))
-diff(cos(y),x)
-diff(y*cos(x),x,y)
[4,3,2,1]
seq(j,j,1,4,-1)
[5-k$k=1..4]
seq(5-k,k,1,4)
cumSum(4,-1,4)
revlist([k$(k=1..4)]
[1,2,4,8]
seq(2^k,k,1,3)
2^[k$(k=0..3)]
2^seq(0,3,1)
[2^k$(k=0..3)]
[2^k$k=0..3]
polygone(0,1,i)
quadrilatere(0,1,1+i
parallelogram(0,1,i)
losange(0,1,pi/2)
polygone(0,1,1+i,i)
![]()
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales