Corrigé du devoir

Questions de cours :  

1. Le logiciel n'effectue la simplification que si on le lui demande.
   simplify(sqrt(a^2-2*a*b+b^2)) retourne abs(a-b). Pour obtenir a-b, il faut saisir l'hypothèse assume(a>b).
2. Dans la première commande, la valeur numérique est calculée d'abord. Les calculs étant effectués par défaut avec une précision de $10^{-14}$, l'écart entre la valeur exacte et la valeur numérique de $10^{15}\pi$ est important, ce qui explique que l'image par la fonction sinus soit loin de 0. Dans la seconde commande au contraire, le calcul de $\sin(10^{15}\pi)$ est exact, et donne donc la valeur 0, dont la valeur numérique est $0.0$.
3. L'exécution de f:=x^2 affecte l'expression $x^2$ à la variable $f$ mais ne définit pas une fonction. Pour obtenir 4, il faudrait définir la fonction $f$ par
   f:=unapply(x^2,x); ou bien
   f:=x->x^2;.
   À partir de l'expression $x^2$, on peut aussi substituer la valeur 2 à $x$ :
   f:=x^2; subs(f,x,2);
4. La commande [a$10] crée la liste composée par l'élément a répété 10 fois. Sa taille est donc 10. À partir de la séquence où a est répété 10 fois, la commande %{a$10%} crée un ensemble, dont les éléments sont tous différents. Sa taille est donc 1.
5. Par défaut, diff calcule la dérivée partielle d'une expression par rapport à la variable $x$. Dans le premier cas, on obtient $2xy^2$, dans le second cas on obtient 0, car la variable $x$ n'apparaît pas dans l'expression. Pour obtenir le gradient, il faut utiliser grad, en spécifiant les variables : grad(x^2*y^2,[x,y]).

Exercice :  

1. assume(x>0);
   simplify(atan(1/x)+atan(x));
   assume(x<0);
   simplify(atan(1/x)+atan(x));
   

2. assume(a>0); assume(b>0); assume(c>0);
   simplify(subs(atan(1/(a+b))+atan(1/(a+c)),c=(1+a^2)/b))
   

3. simplify(atan(1/(a+1))+atan(1/(a^2+a+1)))
   

4. La fonction suivante utilise apply pour transformer les listes:

   Machin(n):={
     local a,l,j,x;
     a:=[1]; l:=a;
     for (j:=0;j<n;j++)
       {
         l:=apply(x->x+1,a);
         a:=apply(x->x^2+x+1,a);
         a:=append(a,op(l));
       }     
   return(a);
   };
   

   Voici une fonction récursive, qui retourne une séquence.

   Machin(a,n):={
   local b,c;
   b:=a+1;
   c:=a^2+a+1;
   if (n==1) return b,c;
   return machin1(b,n-1),machin1(c,n-1);
   }
   :;
   

5. l:=Machin(3)
   simplify(sum(apply(x->atan(1/x),l)))
   

6. taylor_atan(n):=convert(taylor(atan(x),x=0,2*n+1),polynom);
   

   ou

   taylor_atan(n):=truncate(taylor(atan(x),x=0,2*n+1),2*n+1);
   

   ou

   taylor_atan(n):={
     local s,P;
     s:=series(atan(x),x,0,2*n+1);
     P:=convert(s,polynom);   
   return(P);
   }:;
   

7. P14:=unapply(taylor_atan(14),x);
   s1:=sum(apply(x->P14(1/x),l));
   

8. Digits:=25;
   evalf(pi/4-s1);
   

9. simplify(atan(1)-4*atan(1/5)+atan(1/239));
   

10. u:=1+5*i; arg(u);
    v:=1+239*i); arg(v);
    -4*arg(u)+arg(v); 
    simplify(arg(u^{-4}*v));
    

    Les deux calculs d'argument donnent la même valeur : $3\pi/4$.
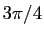11. De la formule
    $$\frac{3\pi}{4}=-4*\arctan(5)+\arctan(239)$$
    obtenue à la question précédente, on passe à la formule de Machin par
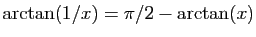    $\arctan(1/x)=\pi/2-\arctan(x)$ (question 1).
12. s2:=4*P14(1/5)-P14(1/239)
13. evalf(pi/4-s2)

14. c:=[44,7,-12,24]; v:=[57,239,682,12943];
    simplify(c*apply(x->atan(1/x),v));
    s3:=c*apply(x->P14(1/x),v);
    Digits:=60;
    evalf(pi/4-s3);
    

15. c:=[12,32,-5,12]; v:=[49,57,239,110443];
    simplify(c*apply(x->atan(1/x),v));
    s4:=c*apply(x->P14(1/x),v);
    evalf(pi/4-s4);