Il y a souvent plusieurs manières d'obtenir le même résultat en
Xcas. On s'efforcera de choisir les solutions les plus compactes.
Exercice 1
Vérifier les identités suivantes.
-
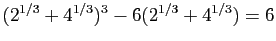
-
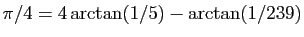
-
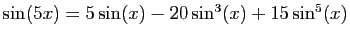
-
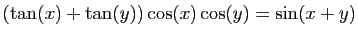
-
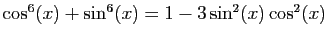
-
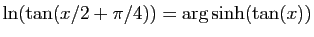
Exercice 2
Transformer la fraction rationnelle
en les fractions suivantes
Exercice 3
Transformer la fraction rationnelle
en les fractions suivantes
Exercice 4
On considère les fonctions 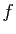 définies par
définies par
Pour chacune de ces fonctions :
- Calculer une primitive
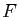 .
.
- Calculer
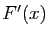 et montrer que
et montrer que
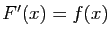 après simplifications.
après simplifications.
Exercice 5
On considère les intégrales définies
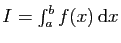 suivantes.
suivantes.
Pour chacune de ces intégrales :
- Calculer la valeur exacte, puis approchée de l'intégrale
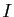 .
.
- Pour
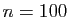 , puis
, puis 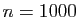 , et
pour tout
, et
pour tout
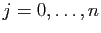 , on pose
, on pose
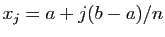 , et
, et
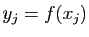 .
Calculer la valeur approchée de l'intégrale
.
Calculer la valeur approchée de l'intégrale 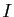 par la
méthode des rectangles à gauche :
par la
méthode des rectangles à gauche :
- Même question avec la méthode des trapèzes :
Exercice 7
On considère l'équation
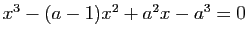 comme une
équation en
comme une
équation en 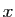 .
.
- Représenter graphiquement la solution
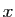 en fonction de
en fonction de 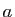 à l'aide
de la fonction
à l'aide
de la fonction
plotimplicit.
- Calculer les trois solutions de l'équation, en utilisant
rootof
pour la première, en éliminant la première avec quo et en
trouvant les deux dernières solutions en résolvant l'équation
du second degré (utiliser coeff pour calculer le discriminant
de l'équation).
- Représenter graphiquement chacune des
trois racines sur le même graphique avec une couleur
différente, et pour les valeurs de
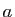 telles que ces solutions soient réelles (on pourra utiliser
telles que ces solutions soient réelles (on pourra utiliser
resultant pour trouver les valeurs de 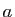 pour lesquelles
l'équation possède une racine multiple en
pour lesquelles
l'équation possède une racine multiple en 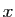 , ces valeurs
sont les bornes possibles des intervalles en
, ces valeurs
sont les bornes possibles des intervalles en 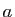 où chacune des
racines sont réelles).
où chacune des
racines sont réelles).
- Donner la valeur des
solutions pour
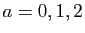 .
.
Exercice 8
On considère les limites suivantes.
Pour chacune d'entre elles :
- Donner sa valeur exacte.
- Trouver une valeur de
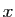 telle que la distance de
telle que la distance de 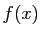 à la
limite soit inférieure à
à la
limite soit inférieure à 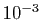 .
.
Exercice 9
Représenter les fonctions 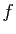 suivantes, en choisissant l'intervalle
des abscisses et des ordonnées, de façon à obtenir
la représentation la plus informative possible.
suivantes, en choisissant l'intervalle
des abscisses et des ordonnées, de façon à obtenir
la représentation la plus informative possible.
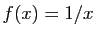 .
.
-
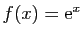 .
.
-
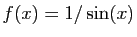 .
.
-
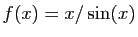 .
.
-
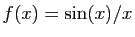 .
.
Exercice 10
On considère la fonction
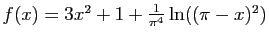 .
.
- Vérifier que cette fonction prend des valeurs négatives sur
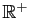 . Représenter la fonction sur l'intervalle
. Représenter la fonction sur l'intervalle ![$ [0,5]$](img135.gif) .
.
- Déterminer
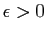 tel que Xcas donne une représentation
correcte de la fonction sur l'intervalle
tel que Xcas donne une représentation
correcte de la fonction sur l'intervalle
![$ [\pi-\epsilon,\pi+\epsilon]$](img137.gif) .
.
Exercice 11
- Représenter la fonction
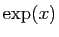 sur l'intervalle
sur l'intervalle ![$ [-1,1]$](img139.gif) .
Sur ce graphique, tracer aussi les représentations
des polynômes de Taylor de cette fonction en
.
Sur ce graphique, tracer aussi les représentations
des polynômes de Taylor de cette fonction en 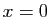 , aux ordres
, aux ordres
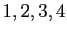 .
.
- Même question pour l'intervalle
![$ [1,2]$](img142.gif) .
.
- Représenter la fonction
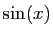 sur l'intervalle
sur l'intervalle
![$ [-\pi,\pi]$](img144.gif) . Sur
le même graphique, superposer les représentations
des polynômes de Taylor de cette fonction en
. Sur
le même graphique, superposer les représentations
des polynômes de Taylor de cette fonction en 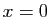 , aux ordres
, aux ordres
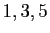 .
.
Exercice 12
Superposer les représentations suivantes sur le même graphique,
allant de 0 à 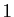 en abscisse et en ordonnée.
en abscisse et en ordonnée.
- La première bissectrice (
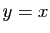 ).
).
- Le graphe de la fonction
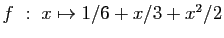 .
.
- La tangente à la fonction
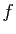 au point
au point 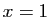 .
.
- Un segment vertical allant de l'axe des
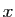 au
point d'intersection de la fonction
au
point d'intersection de la fonction 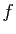 et de
la première bissectrice, et
un segment horizontal allant de ce point d'intersection
à l'axe des
et de
la première bissectrice, et
un segment horizontal allant de ce point d'intersection
à l'axe des 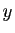 .
.
- Les chaînes de caractères
"point fixe" et "tangente", positionnées sur le
graphique.
Exercice 13
Le but de l'exercice est de représenter sur un même graphique
des familles de fonctions. On choisira le nombre de courbes, l'intervalle
de représentation, les échelles en 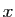 et
et 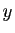 ainsi que le
pas de discrétisation des abscisses, de façon à obtenir
la représentation la plus informative possible.
ainsi que le
pas de discrétisation des abscisses, de façon à obtenir
la représentation la plus informative possible.
- Fonctions
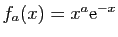 , pour
, pour 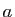 allant de
allant de 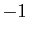 à
à 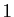 .
.
- Fonctions
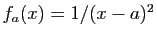 , pour
, pour 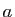 allant de
allant de 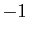 à
à 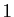 .
.
- Fonctions
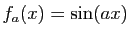 , pour
, pour 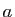 allant de 0 à
allant de 0 à 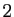 .
.
Exercice 14
Pour chacune des courbes paramétrées suivantes, on choisira un
intervalle de valeurs du paramètre
assurant une représentation complète et suffisamment lisse.
Exercice 15
Le but de l'exercice est de visualiser de différentes manières
la surface définie par
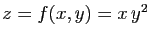 . Ouvrir une fenêtre
de géométrie 3-d.
. Ouvrir une fenêtre
de géométrie 3-d.
- Choisir un domaine de représentation et les pas de discrétisation,
de manière à obtenir une représentation informative
avec
plotfunc.
- Créer un paramètre
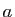 modifiable à la souris
avec la fonction
modifiable à la souris
avec la fonction assume.
Représenter la courbe définie par 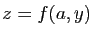 , puis faites
varier le paramètre à la souris.
, puis faites
varier le paramètre à la souris.
- Créer un paramètre
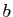 modifiable à la souris.
Représenter la courbe définie par
modifiable à la souris.
Représenter la courbe définie par 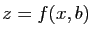 , puis faites
varier le paramètre à la souris.
, puis faites
varier le paramètre à la souris.
Exercice 16
Le but de l'exercice est de visualiser un cône de différentes
manières.
- Représenter la surface d'équation
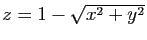 .
.
- Représenter la surface paramétrée définie par :
- En choisisant une valeur de
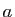 suffisamment grande, représenter la courbe
paramétrée définie par :
suffisamment grande, représenter la courbe
paramétrée définie par :
- Représenter la famille de courbes paramétrées définies par :
- Représenter le même cône en utilisant la fonction
cone.
Exercice 17
- Engendrer une liste
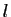 de
de 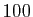 entiers au hasard entre
entiers au hasard entre 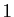 et
et 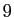 .
.
- Vérifier que l'ensemble des valeurs de
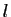 est contenu dans
est contenu dans
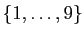 .
.
- Extraire de la liste
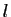 toutes les valeurs
toutes les valeurs
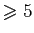 .
.
- Pour tout
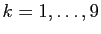 , compter combien de valeurs de la liste
, compter combien de valeurs de la liste 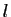 sont égales à
sont égales à 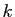 .
.
Exercice 19
Écrire (sans utiliser de boucle) les séquences suivantes :
- Nombres de
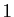 à
à 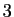 par pas de
par pas de 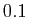 .
.
- Nombres de
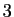 à
à 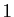 par pas de
par pas de 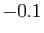 .
.
- Carrés des
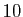 premiers entiers.
premiers entiers.
- Nombres de la forme
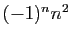 pour
pour
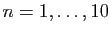 .
.
- 10 "0" suivis de 10 "1".
- 3 "0" suivis de 3 "1", suivis de 3 "2",...,
suivis de 3 "9".
- "1", suivi de 1 "0", suivi de "2", suivi de 2 "0",...
, suivi de "8", suivi de 8 zéros, suivi de "9".
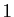 "
"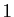 " suivi de
" suivi de 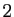 "
"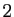 ", suivis de
", suivis de 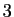 "
"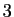 ",...,
suivis de
",...,
suivis de 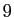 "
"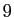 ".
".
Exercice 21
- Écrire la matrice carrée
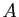 d'ordre
d'ordre 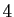 , telle que
, telle que 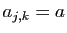 si
si 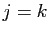 et
et
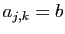 si
si 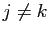 , où
, où 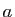 et
et 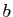 sont des variables.
sont des variables.
- Calculer et factoriser le polynôme caractéristique de
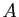 .
.
- Déterminer une matrice orthogonale
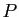 telle que
telle que
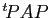 soit
une matrice diagonale.
soit
une matrice diagonale.
- Utiliser la question précédente pour définir la fonction
qui à un entier
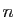 associe la matrice
associe la matrice 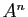 .
.
- Calculer
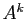 , pour
, pour
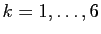 en effectuant les produits
matriciels, et vérifier que la fonction définie à la question
précédente donne bien le même résultat.
en effectuant les produits
matriciels, et vérifier que la fonction définie à la question
précédente donne bien le même résultat.
Exercice 23
Écrire les fonctions suivantes, sans utiliser de boucle.
- La fonction
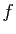 prend en entrée un entier
prend en entrée un entier 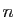 et deux réels
et deux réels 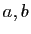 et retourne
la matrice
et retourne
la matrice 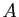 dont les termes diagonaux valent
dont les termes diagonaux valent 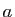 , tous les autres
termes étant égaux à
, tous les autres
termes étant égaux à 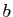 .
.
- La fonction
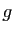 prend en entrée un entier
prend en entrée un entier 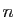 et trois réels
et trois réels 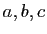 et retourne
la matrice
et retourne
la matrice
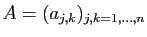 dont les termes diagonaux
sont égaux à
dont les termes diagonaux
sont égaux à 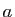 , les termes
, les termes 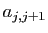 égaux à
égaux à 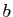 et
termes
et
termes 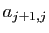 égaux à
égaux à 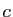 , pour
, pour
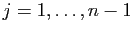 (les autres
termes sont nuls).
(les autres
termes sont nuls).
- La fonction
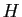 prend en entrée un entier
prend en entrée un entier 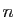 et retourne en sortie
la matrice
et retourne en sortie
la matrice
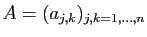 définie par
définie par
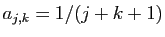 (matrice de Hilbert).
Comparer le temps d'exécution de votre fonction avec celui de
la fonction
(matrice de Hilbert).
Comparer le temps d'exécution de votre fonction avec celui de
la fonction hilbert.
- La fonction
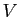 prend en entrée un vecteur
prend en entrée un vecteur
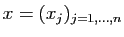 et retourne en sortie la matrice
et retourne en sortie la matrice
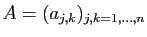 définie par
définie par
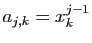 (matrice de Vandermonde).
Comparer le temps d'exécution de votre fonction avec celui de
la fonction
(matrice de Vandermonde).
Comparer le temps d'exécution de votre fonction avec celui de
la fonction vandermonde.
- La fonction
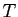 prend en entrée un vecteur
prend en entrée un vecteur
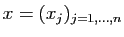 et retourne en sortie la matrice
et retourne en sortie la matrice
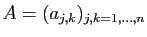 définie par
définie par
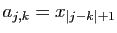 (matrice de Toeplitz).
(matrice de Toeplitz).
Exercice 24
Écrire les fonctions suivantes. Toutes prennent en entrée une fonction
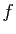 (de
(de
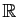 dans
dans
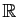 ), et trois valeurs
), et trois valeurs 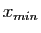 ,
,
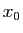 et
et 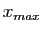 (supposées telles que
(supposées telles que
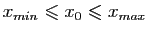 ).
).
derive :
Elle calcule et représente graphiquement
la dérivée de 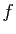 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img229.gif) . Elle retourne la
valeur de
. Elle retourne la
valeur de 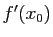 .
.
tangente :
Elle représente la fonction 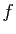 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img229.gif) , elle
superpose sur le même graphique la tangente à
, elle
superpose sur le même graphique la tangente à 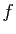 au point
au point 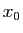 , et
retourne l'équation de cette tangente comme un polynôme du premier
degré.
, et
retourne l'équation de cette tangente comme un polynôme du premier
degré.
araignee :
Elle représente la fonction 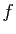 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img229.gif) ,
ainsi que la droite d'équation
,
ainsi que la droite d'équation 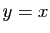 (première bissectrice).
Elle calcule et retourne les
(première bissectrice).
Elle calcule et retourne les 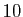 premiers itérés de
premiers itérés de 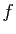 en
en 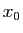 (
(
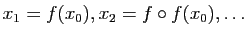 ). Elle représente la suite de
segments, alternativement verticaux et horizontaux, permettant de visualiser
les itérations : segments joignant
). Elle représente la suite de
segments, alternativement verticaux et horizontaux, permettant de visualiser
les itérations : segments joignant 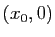 ,
, 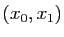 ,
, 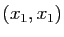 ,
,
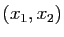 ,
, 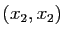 , ...
(comparer avec la fonction
, ...
(comparer avec la fonction plotseq).
newton_graph :
Elle représente la fonction 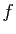 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img229.gif) .
Elle calcule et retourne les dix premiers itérés de la suite définie
à partir de
.
Elle calcule et retourne les dix premiers itérés de la suite définie
à partir de 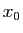 par la méthode de Newton :
par la méthode de Newton :
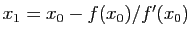 ,
,
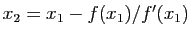 ... Les valeurs de la dérivée sont
approchées. La fonction représente sur le même graphique les
segments permettant de visualiser les itérations : segments joignant
... Les valeurs de la dérivée sont
approchées. La fonction représente sur le même graphique les
segments permettant de visualiser les itérations : segments joignant
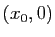 ,
,
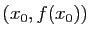 ,
, 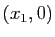 ,
,
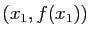 ,
, 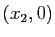 ,
,
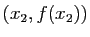 ,...
(comparer avec la fonction
,...
(comparer avec la fonction newton)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
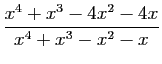
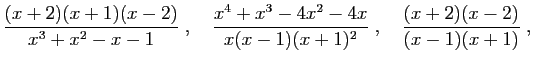
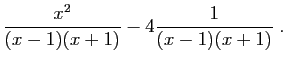
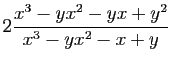
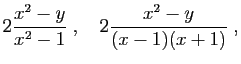
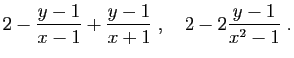
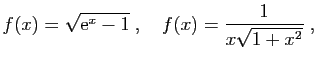
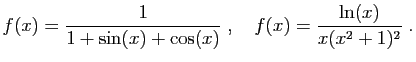
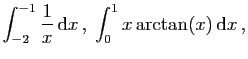
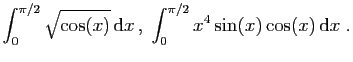
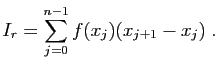
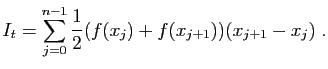
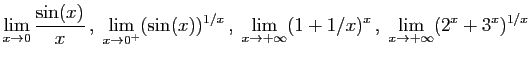
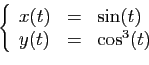
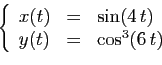
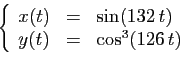
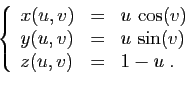
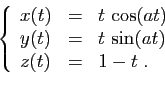
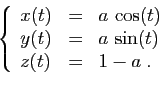
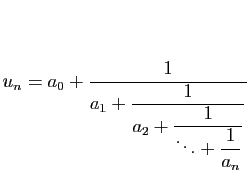
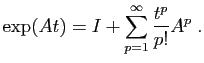
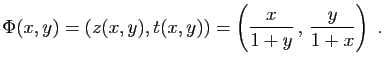
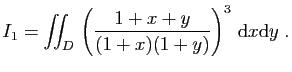
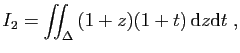
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales