v formé
de tous les entiers de -
v=linspace(1,100,100)-
v=[1:0.1:100]-
v=[]; for i=1:100, v=[v,i]; end; v-
v=1; for i=1:100, v=[v,i+1]; end; v-
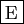
v=[1;1;100]
v formé
de tous les entiers de v=linspace(1,100,100)
v=[1:0.1:100]
v=[]; for i=1:100, v=[v,i]; end; v
v=1; for i=1:100, v=[v,i+1]; end; v
v=[1;1;100]
A=[1:4;4:-1:1;0:3] et v=[2;2;3].
v'*A*v retourne un réel.
v*v' retourne une matrice à trois
lignes et trois colonnes.
v(3:-1:1)'==A(3,:) retourne [T T T]'
v(3:-1:1)'==A(:,3) retourne [T T T]'
B=A'; B(:,3)==v retourne [T T T]
A=[0:3;3:-1:0]+%i*[1:4;4:-1:1].
La ligne de commande proposée affiche une matrice réelle
à deux lignes et quatre colonnes.
A.'
A*conj(A)
real(A)
abs(A)
real(A)<imag(A)
R=[-2,-2,2,2].
La ligne de commande proposée affiche un rectangle.
x=[-1,1,1,-1,-1];y=[-1,-1,1,1,-1]; plot2d(x,y,rect=R);
x=[-1,-1,1,1];y=[-1,1,-1,1]; plot2d(x,y,rect=R);
x=[-1,-1,1]';y=[-1,1,1]'; plot2d([x,y],[y,x],style=[1,1],rect=R)
x=[-1,-1,1];y=[-1,1,1]; plot2d([x,y],[y,x],style=[1,1],rect=R)
x=[-1,-1,1,1;-1,1,1,-1]; y=[-1,1,1,-1;1,1,-1,-1]; plot2d(x,y,style=[1,1,1],rect=R);
e=0.1; x=linspace(e,%pi-e,200); x=[x'-%pi,x']; y=(1)./sin(x); plot2d(x,y,style=[5,5]);
x=[0:0.001:%pi]; x=[x'-%pi,x']; y=(1)./sin(x); plot2d(x,y,style=[5,5]);
x=[-%pi:%pi]; y=(1)./sin(x); plot(x,y);
x=[-%pi+0.1:0.1:%pi-0.1]; y=1/sin(x); plot(x,y);
x=[0.1:0.01:%pi-0.1]'; y=(1)./sin(x); plot2d([x-%pi,x],[-y,y],style=[5,5]);
x=linspace(-%pi,%pi,50)'; y=[]; for i=-1:1, y=[y,sin(x.*i)]; end; plot2d([x,x,x],y);
x=linspace(-%pi,%pi,50)'; y=[sin(-x),zeros(50,1),sin(x)]; plot2d([x,x,x],y,style=[1,2,3]);
A une matrice. La ligne de commande proposée définit la
matrice B dont le coefficient d'ordre A si B=kron(A,[0;1])
B=A; for i=2:n, B(i,:)=0
B=zeros(A); for i=1:2:size(A,"r"), B(i,:)=A(i,:); end;
B=A; n=size(A,"r"); B(find((-1)^[1:n]==-1,:)=0
B=(A+A*ones(-A))/2
f.sci,
dans le répertoire courant. La commande
getf("f.sci") permet de définir la fonction f qui à
deux matrices A et B de même taille
associe la matrice f(A,B) dont le coefficient d'ordre A et B.
f(A,B)=min(A,B)
function C=f(A,B)
C=min(A,B);
endfunction
deff("f(A,B)","min(A,B)")
function C=f(A,B)
for i=1:size(A), C(i)=min(A(i),B(i));
endfunction
function C=f(A,B)
C=B; C(A<B)=A(A<B);
endfunction
moins qui
retourne la différence de deux matrices de même taille
f.sci les lignes
function C=f(A,B) C=A-B; endfunctionpuis charger le fichier par
getf("f.sci").
f.sci la ligne
deff("C=moins(A,B)","C=A-B")
puis charger le fichier par getf("f.sci").
f.sci les lignes
function C=f(A,B) for i=1:n, for j=1:n, C(i,j)=A(i,j)-B(i,j); end; end; endfunctionpuis charger le fichier par
getf("f.sci").
f.sci les lignes
function C=f(A,B) C=A-B endfunctionpuis charger le fichier par
getf("f.sci").
f.sce la ligne
deff("C=moins(A,B)","C=A-B")
puis charger le fichier par exec("f.sce").
integrate("sqrt(x)","x",0,10)
t=[0,10]; inttrap(t,sqrt(t))
t=[0:0.001:10]; inttrap(t,sqrt(t))
t=[0:0.001:10]; cumsum(sqrt(t))
t=[0:0.001:10]; sum(sqrt(t)/0.001)
![]()
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales