Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours :
On désigne par 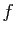 la fonction qui à
la fonction qui à
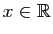 associe
associe
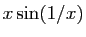 (prolongée par continuité en 0). Le but de l'exercice
est d'en obtenir une représentation graphique sur un intervalle contenant
0, qui puisse être agrandie par zoom au voisinage de 0.
(prolongée par continuité en 0). Le but de l'exercice
est d'en obtenir une représentation graphique sur un intervalle contenant
0, qui puisse être agrandie par zoom au voisinage de 0.
- Expliquer les raisons pour lesquelles les lignes de commandes suivantes
ne conviennent pas, quelle que soit la valeur de
n.
x=linspace(-1,1,n); y=x*sin(1/x);
plot2d(x,y)
- On note
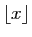 la partie entière du nombre réel
la partie entière du nombre réel 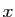 . Soit
. Soit 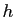 un paramètre réel strictement positif. Définir le vecteur
un paramètre réel strictement positif. Définir le vecteur
x de valeurs allant de
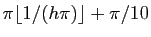 à
à
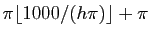 par pas de
par pas de 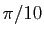 . Définir le vecteur
. Définir le vecteur
X des inverses des valeurs de x, puis le vecteur Y,
produit des valeurs de 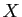 par les sinus de celles de
par les sinus de celles de x.
Expliquer en quoi la commande plot2d(X,Y) constitue une
représentation graphique satisfaisante de 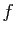 , et préciser
l'intervalle de représentation.
, et préciser
l'intervalle de représentation.
- Comment en déduire une représentation satisfaisante
sur
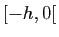 ?
?
- On souhaite utiliser ce qui précède pour obtenir une représentation sur
![$ [-h,h]$](img250.gif) . Donner les limites du cadre graphique.
. Donner les limites du cadre graphique.
- Écrire une fonction qui prend en entrée
un paramètre
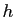 strictement positif, qui retourne en
sortie
strictement positif, qui retourne en
sortie 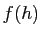 et représente la fonction
et représente la fonction 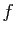 sur l'intervalle
sur l'intervalle ![$ [-h,h]$](img250.gif) .
.
Exercice 1 :
Soient
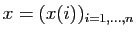 et
et
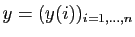 deux
vecteurs. On appelle suite des différences divisées de
deux
vecteurs. On appelle suite des différences divisées de 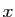 par
par 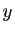 la suite de vecteurs
la suite de vecteurs
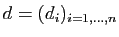 , définie par
, définie par 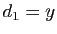 , et pour
, et pour
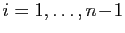 ,
,
- Définir la fonction
differences_divisees,
qui prend en entrée deux vecteurs lignes x
et y de même taille, et qui retourne en sortie la matrice
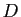 , triangulaire inférieure dont les lignes sont les
vecteurs de différences
, triangulaire inférieure dont les lignes sont les
vecteurs de différences 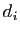 , complétés par des zéros.
, complétés par des zéros.
- Soit
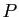 un polynôme de degré
un polynôme de degré
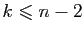 .
On pose
.
On pose
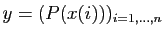 . Vérifiez expérimentalement
que le vecteur
. Vérifiez expérimentalement
que le vecteur 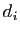 est constant
pour
est constant
pour 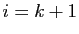 , et nul pour
, et nul pour
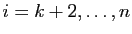 .
.
- Définir la fonction
Newton, qui prend en entrée deux vecteurs
lignes x et y de même taille, et qui retourne en sortie
le polynôme 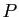 , de degré
, de degré 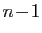 , défini par :
, défini par :
- Vérifiez expérimentalement que
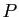 est le
polynôme interpolateur de Lagrange des
ordonnées
est le
polynôme interpolateur de Lagrange des
ordonnées 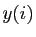 aux abscisses
aux abscisses 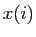 :
:
- Le polynôme interpolateur de Lagrange
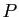 peut se calculer
aussi par la formule suivante :
peut se calculer
aussi par la formule suivante :
Définir la fonction Lagrange, analogue à la fonction
Newton, mais utilisant la nouvelle formule.
- Vérifiez expérimentalement que
Lagrange est
à la fois plus lente et plus instable numériquement
que Newton.
Exercice 2 :
Étant donnée une matrice symétrique définie positive
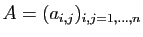 , sa
décomposition de Cholesky consiste à écrire
, sa
décomposition de Cholesky consiste à écrire
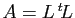 , où
, où 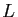 est une matrice triangulaire inférieure.
Pour obtenir la matrice
est une matrice triangulaire inférieure.
Pour obtenir la matrice
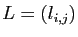 ,
on définit d'abord sa première colonne :
,
on définit d'abord sa première colonne :
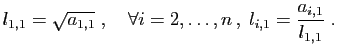
Pour
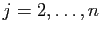 , la
, la 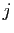 -ième colonne est définie à partir des précédentes :
-ième colonne est définie à partir des précédentes :
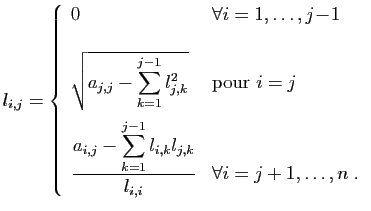
- Définir une fonction
Lt qui prend en entrée un entier strictement
positif 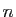 et retourne en sortie la matrice
et retourne en sortie la matrice L de
taille 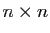 dont le coefficient d'ordre
dont le coefficient d'ordre 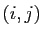 est nul si
est nul si 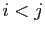 , égal à
, égal à 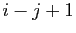 sinon.
sinon.
- Définir une fonction
Lr qui prend en entrée un entier strictement
positif 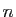 et retourne en sortie la matrice
et retourne en sortie la matrice L de
taille 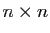 dont le coefficient d'ordre
dont le coefficient d'ordre 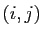 est nul si
est nul si 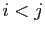 , égal à un nombre
au hasard entre 0 et
, égal à un nombre
au hasard entre 0 et 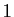 sinon.
sinon.
- Pour
L=Lt(n) et L=Lr(n),
calculer la matrice A égale au produit
de L par sa transposée, puis la norme matricielle de la
différence entre L' et chol(A).
Noter le temps d'exécution de la commande chol(A).
Effectuez des essais pour différentes valeurs de n et
notez vos observations.
- Définir la fonction
Cholesky3, qui prend en entrée une matrice
symétrique A, et qui retourne en sortie la matrice triangulaire
inférieure L, en utilisant 3 boucles emboîtées : la première
pour l'indice de colonne, la seconde pour l'indice de ligne, la troisième
pour calculer la somme définissant le numérateur de 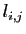 .
.
- Répéter les expériences de la question 3 en remplaçant
la fonction Scilab
chol par Cholesky3.
- Modifier la fonction
Cholesky3 en Cholesky2
et remplacer la troisième boucle par un
calcul utilisant sum.
- Répéter les expériences de la question 3 en renplaçant
chol par Cholesky2.
- Modifier la fonction
Cholesky2 en Cholesky1
et remplacer la deuxième boucle par un
calcul direct de la 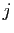 -ième colonne.
-ième colonne.
- Répéter les expériences de la question 3 en renplaçant
chol par Cholesky1.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() la fonction qui à
la fonction qui à
![]() associe
associe
![]() (prolongée par continuité en 0). Le but de l'exercice
est d'en obtenir une représentation graphique sur un intervalle contenant
0, qui puisse être agrandie par zoom au voisinage de 0.
(prolongée par continuité en 0). Le but de l'exercice
est d'en obtenir une représentation graphique sur un intervalle contenant
0, qui puisse être agrandie par zoom au voisinage de 0.
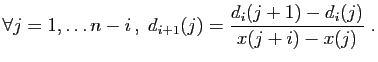
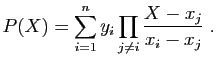
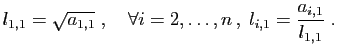
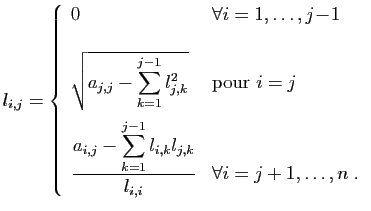
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales