v
le vecteur des entiers consécutifs de -
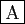
v <- seq(1,1,10)-
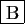
v <- (0:1)-
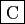
v <- sort(sample(1:10,10))-
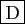
v <- 1; for (i in 2:10){append(v,i)}-
v <- rep(1,10); while (i<=10){v[i] <- i}
v
le vecteur des entiers consécutifs de v <- seq(1,1,10)
v <- (0:1)
v <- sort(sample(1:10,10))
v <- 1; for (i in 2:10){append(v,i)}
v <- rep(1,10); while (i<=10){v[i] <- i}
diag(rep(1,2))
identity(2,2)
rbind(c(1,0),c(0,1))
1:0%*%t(0:1)+0:1%*%t(1:0)
toeplitz(c(0,1))
as.vector(table(factor(x,levels=0:1)))
which(x==c(0,1))
ifelse(x==0,yes=1,no=0)
tabular(x)
c(length(x)-sum(x),sum(x))
barplot(table(x))
plot(table(x))
hist(x)
barplot(x)
plot(x)
quantile(x,c(0.25,0.5,0.75))
as.vector(quantile(x,(1:3)/4))
sort(x)[length(x)*(1:3)/4]
x[floor(length(x)*(1:3)/4)]
as.numeric(quantile(x,0.25*c(1,2,3)))
ifelse(runif(10)<1/3,yes=0,no=1)
rbinom(10,1,1/3)
sample(c(0.1),10,replace=T)
ifelse(rgeom(10,0.3)==0,yes=1,no=0)
floor(runif(10,0,3))
pt(0,3)
dbinom(0,1,1/2)
qt(0)
qnorm(0)
pchisq(2,2)
moins qui à un couple
de vecteurs associe sa différence.
function <- moins(x,y){return(u-v)}
moins <- function{return(u-v)}
moins <- function(u,v){return(u-v)}
function moins(u,v){return(u-v)}
moins <- function(u,v)u-v
mean(x)+sd(x)*qnorm(0.025,0.975)/sqrt(length(x))
mean(x)+sd(x)*qnorm(0.975)*c(-1,1)
as.vector(t.test(x)$conf.int)
mean(x)+sd(x)*qnorm(0.975)*c(-1,1)/sqrt(length(x))
t.test(x)$conf.int
t.test(x,mu=1,alternative="less")$p.value
pnorm(sqrt(length(x))*(mean(x)-1)/sd(x))
1-pnorm(sqrt(length(x))*mean(x)/sd(x))
t.test(x,alternative="less")$p.value
pnorm((mean(x)-1)/(sd(x)*length(x)))
![]()
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales