Devoir

Essayez de bien rédiger vos réponses, sans vous reporter ni au cours, ni au corrigé. Si vous souhaitez vous évaluer, donnez-vous trois heures ; puis comparez vos réponses avec le corrigé et comptez un point pour chaque question à laquelle vous aurez correctement répondu.

Questions de cours :

Tirer un échantillon de taille de la loi exponentielle $\mathcal{E}(1)$ . Calculer la moyenne et l'écart-type empiriques, ainsi que les quantiles d'ordre , , .
Représenter un histogramme des valeurs obtenues en bleu. Superposer sur le même graphique une estimation de la densité en vert et la densité exacte de la loi $\mathcal{E}(1)$ en rouge.
Représenter la fonction de répartition empirique de en bleu. Superposer sur le même graphique la fonction de répartition théorique en rouge.
On considère l'échantillon des parties entières des valeurs de . Calculer la table de fréquence des valeurs observées, puis représenter un diagramme en bâtons en bleu. Juxtaposer sur le même graphique les probabilités de la loi géométrique de paramètre $1-\exp(-1)$ , en rouge.
Appliquer le test de Kolmogorov-Smirnov bilatéral pour tester l'ajustement de l'échantillon à la loi $\mathcal{E}(1)$ . Extraire du résultat la p-valeur.

Problème : Soit $(X_1,\ldots,X_n)$ un échantillon de la loi exponentielle $\mathcal{E}(\lambda)$ , de densité $\lambda\mathrm{e}^{-\lambda x}$ sur $\mathbb{R}^+$ . L'estimateur du maximum de vraisemblance pour $\lambda$ est noté

. C'est l'inverse de la moyenne empirique :

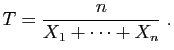
$\displaystyle T = \frac{n}{X_1+\cdots+X_n}\;.$

On admettra que l'espérance de

vaut $\lambda n/(n-1)$ , et que $n\lambda/T$ suit la loi gamma ${\cal G}(n,1)$ . On note

l'estimateur sans biais basé sur

Tirer échantillons de taille de la loi $\mathcal{E}(\lambda)$ , pour $\lambda=2$ . Pour chacun des 1000 échantillons, calculer l'estimation ponctuelle de $\lambda$ par l'inverse de la moyenne empirique, puis la valeur débiaisée. Représenter les estimations de densité de ces deux échantillons d'estimations. Superposer sur le même graphique une ligne verticale donnant la vraie valeur.
Écrire une fonction ic.moy qui prend en entrée un vecteur de données X et un niveau de confiance nc (valeur par défaut ), et qui retourne en sortie un vecteur à deux entrées contenant les bornes de l'intervalle de confiance pour $\lambda$ , déduit de l'intervalle de confiance générique sur la moyenne (fonction t.test).
Écrire une fonction ic.sym qui prend en entrée un vecteur de données X et un niveau de confiance nc (valeur par défaut ), et qui retourne en sortie un vecteur à deux entrées contenant les bornes de l'intervalle de confiance symétrique de niveau nv pour l'échantillon X, basé sur la loi gamma.
Ecrire une fonction test.gamma qui prend en entrée un vecteur de données X et une valeur du paramètre la0, et qui retourne les p-valeurs de 2 tests unilatéraux de l'hypothèse $\mathcal{H}_0 : \lambda=$ la0, contre $\mathcal{H}_1 : \lambda>$ la0. Le premier test est le test de la moyenne (fonction t.test), le second utilise la loi de (fonction pgamma).
On considère deux autres estimateurs de $\lambda$ .

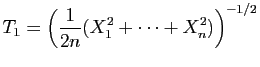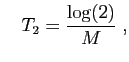
$\displaystyle T_{1} = \left(\frac{1}{2n}(X_1^2+\cdots+X_n^2) \right)^{-1/2}$ et $\displaystyle \quad T_{2} = \frac{\log(2)}{M}\;,$
où désigne la médiane de l'échantillon. Sur les 1000 échantillons de taille 20 de la question 1, calculer les estimations obtenues par , , et . Représenter sur un même graphique les 4 diagrammes en boîte verticaux (fonction boxplot). Représenter la vraie valeur par un trait horizontal.
Tirer un échantillon de taille de la loi $\mathcal{E}(\lambda)$ , pour $\lambda=2$ : . On note $x_1,\ldots,x_{n-1}$ les valeurs de rangées par ordre croissant (statistiques d'ordre, sauf le maximum). Pour tout $i=1,\ldots,n-1$ , on pose $y_i=-\log(1-1/i)$ . Calculer la pente et l'ordonnée à l'origine de la droite de regression linéaire des sur les . Représenter sur un même graphique la droite de régression linéaire et les points de coordonnées .
On appelle la pente de la droite de regression calculée comme dans la question précédente : c'est un nouvel estimateur de $\lambda$ . Écrire une fonction reg.est qui prend en entrée un vecteur de données X, et retourne la valeur de .
Écrire une fonction compare.est, qui prend en entrée une valeur lambda, deux entiers E et n. La fonction tire E échantillons de taille n de la loi exponentielle de paramètre lambda. Elle calcule pour chacun les estimations obtenues par , , , , et . Elle calcule ensuite l'erreur quadratique moyenne des E estimations pour chacun des 5 estimateurs. Elle retourne dans une table ces 5 erreurs quadratiques moyennes.
Tirer deux échantillons de taille de la loi $\mathcal{E}(1)$ : $(X_1,\ldots,X_n)$ et $(Y_1,\ldots,Y_n)$ . Parmi les valeurs du premier échantillon, conserver les valeurs qui vérifient . Soit l'échantillon des valeurs conservées. Représenter un histogramme de l'échantillon . Superposer sur le même graphique la densité de la loi de chi-deux à degré de liberté.
Affecter chaque valeur de du signe ou , choisi avec probabilité . Soit l'échantillon ainsi obtenu. Reésenter la fonction de répartition empirique de l'échantillon . Superposer sur le même graphique la fonction de répartition théorique de la loi $\mathcal {N}(0,1)$ .
Vérifier l'ajustement de l'échantillon à la loi $\mathcal {N}(0,1)$ :
1. par les quantiles (fonction qqnorm),
2. par le test de Shapiro-Wilk (fonction shapiro.test),
3. par le test de Kolmogorov-Smirnov (fonction ks.test).
Simuler trois échantillons de taille de la loi $\mathcal{E}(1)$ : , , . Pour tout $i=1,\ldots,n$ , on pose :

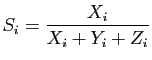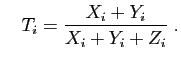
$\displaystyle S_i=\frac{X_i}{X_i+Y_i+Z_i}$ et $\displaystyle \quad T_i=\frac{X_i+Y_i}{X_i+Y_i+Z_i}\;.$
Représenter par des points dans le plan les couples . Vérifier par le test de Kolmogorov-Smirnov, l'ajustement de l'échantillon à la loi bêta $\mathcal{B}(1,2)$ , et l'ajustement de l'échantillon à la loi bêta $\mathcal{B}(2,1)$ .
Simuler deux échantillons de taille de la loi uniforme sur : et . Pour tout $i=1,\ldots,n$ , on pose :

$\displaystyle S'_i=\min\{U_i,V_i\}$ et $\displaystyle \quad T'_i=\max\{U_i,V_i\} \;.$
Vérifier l'ajustement des deux échantillons et d'une part, et d'autre part, par :
1. le test de Kolmogorov-Smirnov
2. le test de Wilcoxon (fonction wilcox.test)
Pour $\lambda=1/2$ , tirer un échantillon de taille de la loi $\mathcal{E}(1/2)$ : . Pour tout $i=1,\ldots,n$ , calculer $p_i=\exp(-T_i)$ , et simuler une variable aléatoire , de loi géométrique de paramètre (le tout sans utiliser de boucle). Représenter les valeurs de l'échantillon par un diagramme en boîte. Calculer les déciles et le maximum.
On admettra que pour tout entier $k\in \mathbb{N}$ , la probabilité que prenne la valeur est $\lambda B((\lambda+1),(k+1))$ , où désigne la fonction beta. Dans l'échantillon , remplacer toutes les valeurs supérieures à 10 par 10. Calculer les probabilités théoriques, puis appliquer le test du chi-deux d'ajustement (fonction chisq.test).