Tous les développement limités de cette section sont au
voisinage de 0.
Pour les obtenir, le premier moyen est de
calculer les dérivées successives et d'en déduire le polynôme
de Taylor. On obtient ainsi les développements suivants, que vous devrez
connaître par c ur.
ur.
Démonstration : Nous avons déjà vu le développement limité de
l'exponentielle : les dérivées successives en 0 sont toutes
égales à 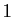 . Nous avions aussi traité le développement de
. Nous avions aussi traité le développement de
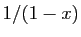 , dont la dérivée
, dont la dérivée 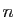 -ième en 0 vaut
-ième en 0 vaut 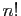 .
Pour le sinus et le cosinus,
.
Pour le sinus et le cosinus,
Les dérivées successives en 0 de 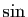 et
et 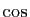 valent
alternativement, 0 et
valent
alternativement, 0 et 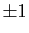 . Précisément :
. Précisément :
![$\displaystyle \sin^{(n)}(0)=\left\{\begin{array}{rcl}
0&\mbox{si}&n\equiv 0 \qu...
...si}&n\equiv 2 \quad[4]\\
-1&\mbox{si}&n\equiv 3 \quad[4]\;,
\end{array}\right.$](img142.gif)
et
![$\displaystyle \quad
\cos^{(k)}(0)=\left\{\begin{array}{rcl}
1&\mbox{si}&n\equiv...
...si}&n\equiv 2 \quad[4]\\
0&\mbox{si}&n\equiv 3 \quad[4]\;.
\end{array}\right.
$](img143.gif)
La figure 3 représente les fonctions sinus et
cosinus avec leurs premiers polynômes de Taylor en 0.
Le point 5 peut être vu comme une généralisation de la
formule du binôme de Newton ; si 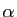 est un entier
positif,
est un entier
positif,
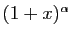 est un polynôme, et tous les termes du
développement sont nuls à partir de
est un polynôme, et tous les termes du
développement sont nuls à partir de
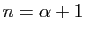 . Dans le cas
général, la dérivée
. Dans le cas
général, la dérivée 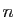 -ième de
-ième de
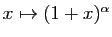 est :
est :
La démontration par récurrence est facile. On en déduit
immédiatement la formule annoncée.
Figure 3:
Fonctions sinus et cosinus avec leurs premiers
polynômes de Taylor en 0.
|
|
Constatez que le développement du sinus ne contient que des termes
impairs, celui du cosinus que des termes pairs. C'est une propriété
générale qui se démontre facilement : si une fonction est paire,
ses dérivées d'ordre impair en 0 sont nulles, donc son
polynôme de Taylor ne contient que des termes pairs ; si la fonction
est impaire, ce sont ses dérivées d'ordre pair qui s'annulent et
le polynôme de Taylor ne contient que des termes impairs.
A partir des cinq développements du théorème 6, on
peut en calculer beaucoup d'autres. Par exemple par
linéarité à partir du développement de l'exponentielle :
Il est à noter que les développements du sinus et cosinus
ordinaires peuvent se retrouver de la même façon en utilisant
les formules d'Euler.
La figure 4 représente les fonctions 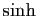 et
et
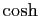 avec leurs premiers polynômes de Taylor en
0. Observez que dans les deux cas, le quatrième polynôme ne se
distingue pas de la fonction sur l'intervalle de représentation.
avec leurs premiers polynômes de Taylor en
0. Observez que dans les deux cas, le quatrième polynôme ne se
distingue pas de la fonction sur l'intervalle de représentation.
Figure 4:
Fonctions sinus et cosinus hyperboliques
avec leurs premiers
polynômes de Taylor en 0.
|
|
Utilisons maintenant le développement de 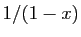 . Par composition
avec
. Par composition
avec
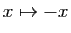 , on obtient :
, on obtient :
La primitive nulle en 0 est 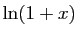 :
:
La figure 5 représente la fonction 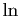 et ses six
premiers polynômes de Taylor.
et ses six
premiers polynômes de Taylor.
Figure:
Fonction 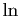 et ses polynômes de Taylor en
0 jusqu'à l'ordre
et ses polynômes de Taylor en
0 jusqu'à l'ordre 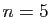 .
.
|
|
Par composition avec
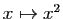 , on obtient aussi :
, on obtient aussi :
La primitive nulle en 0 est
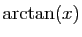 :
:
Utilisons enfin le développement de
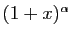 . Pour
. Pour
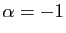 , on retrouve le développement de
, on retrouve le développement de 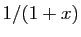 que nous
avons déjà écrit. Les cas les plus
fréquents sont
que nous
avons déjà écrit. Les cas les plus
fréquents sont
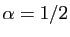 ,
,
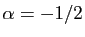 et ceux où
et ceux où 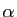 est un entier négatif.
est un entier négatif.
Du développement de
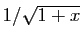 , on déduit celui de
, on déduit celui de
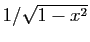 , par composition avec
, par composition avec
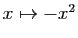 .
La primitive de
.
La primitive de
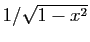 nulle en 0 est
nulle en 0 est
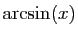 .
.
Pour illustrer les différentes techniques,
nous proposons de calculer le
développement de la fonction
tangente d'ordre 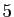 par sept méthodes
différentes. Nous ne détaillons pas tous les calculs : il vous est
vivement conseillé de les reprendre par vous-même.
par sept méthodes
différentes. Nous ne détaillons pas tous les calculs : il vous est
vivement conseillé de les reprendre par vous-même.
Méthode 1 :
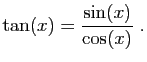
Partez avec les développements limités de 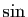 et
et 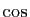 à
l'ordre
à
l'ordre 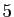 :
:
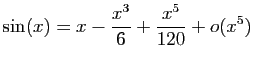
et
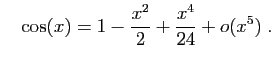
Calculez ensuite le développement de 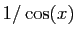 .
(il est inutile d'écrire les termes de degrés supérieurs à
.
(il est inutile d'écrire les termes de degrés supérieurs à 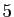 ).
).
Il reste à effectuer le produit par le développement de 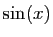 .
.
Méthode 2 :
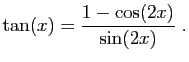
Attention, il y a un piège : si vous procédez comme pour la
méthode précédente, voici ce
que vous trouvez.
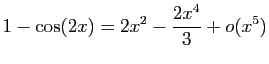
et
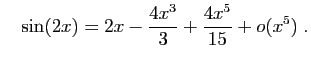
Donc :
Tout ce que vous pourrez en déduire, c'est un développement à
l'ordre 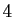 , et non
, et non 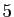 . Pour éviter cela, il faut augmenter
l'ordre au départ.
. Pour éviter cela, il faut augmenter
l'ordre au départ.
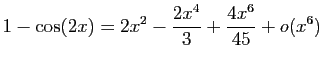
et
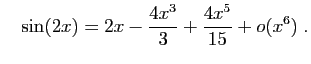
Donc :
Vous calculez séparément :
puis vous effectuez le produit :
Méthode 3 :
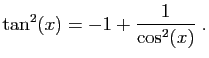
Même piège que précédemment : si vous
partez de développements d'ordre 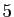 , vous n'obtiendrez
finalement que l'ordre
, vous n'obtiendrez
finalement que l'ordre 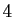 .
Les calculs successifs sont les suivants.
.
Les calculs successifs sont les suivants.
Il peut vous paraître osé d'avoir remplacé
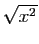 par
par
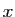 sans se préoccuper du signe :
il se trouve que l'expression obtenue est aussi valable
pour
sans se préoccuper du signe :
il se trouve que l'expression obtenue est aussi valable
pour 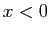 (pensez que la fonction est impaire).
(pensez que la fonction est impaire).
Méthode 4 :
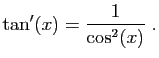
Comme nous prendrons une primitive à la fin, il suffit d'un
développement d'ordre 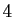 pour la dérivée (ce qui en
l'occurrence ne change pas grand-chose).
pour la dérivée (ce qui en
l'occurrence ne change pas grand-chose).
Il reste à prendre la primitive, en utilisant le fait que le terme
constant est nul.
Méthode 5 :
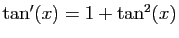 .
.
Nous avons ici une équation dont l'inconnue est le développement
cherché. Comme la fonction tangente est impaire, nous savons que son
développement d'ordre 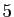 est
de la forme
est
de la forme
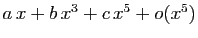 , où
, où 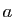 ,
, 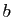 et
et 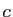 sont des
réels à déterminer. Alors :
sont des
réels à déterminer. Alors :
La primitive nulle en 0 a pour développement :
Par unicité du développement limité, on doit avoir :
On obtient donc : 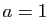 ,
, 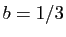 et
et 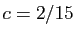 .
.
Méthode 6 :
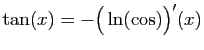 .
.
Comme nous dériverons à la fin, nous devons commencer avec des
développements d'ordre 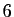 .
.
L'opposé de la dérivée donne bien :
Méthode 7 :
 .
.
Nous connaissons le développement de 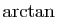 d'ordre
d'ordre 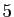 :
:
Soit
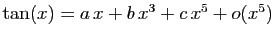 le développement cherché.
Alors :
le développement cherché.
Alors :
Par unicité du développement limité, on doit avoir :
On obtient encore : 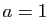 ,
, 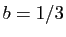 et
et 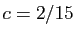 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![$\displaystyle \sin^{(n)}(0)=\left\{\begin{array}{rcl}
0&\mbox{si}&n\equiv 0 \qu...
...si}&n\equiv 2 \quad[4]\\
-1&\mbox{si}&n\equiv 3 \quad[4]\;,
\end{array}\right.$](img142.gif) et
et![$\displaystyle \quad
\cos^{(k)}(0)=\left\{\begin{array}{rcl}
1&\mbox{si}&n\equiv...
...si}&n\equiv 2 \quad[4]\\
0&\mbox{si}&n\equiv 3 \quad[4]\;.
\end{array}\right.
$](img143.gif)
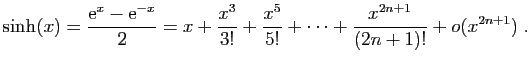
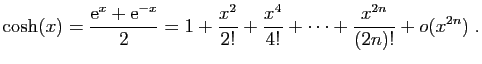
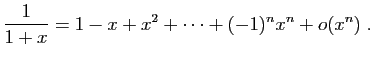
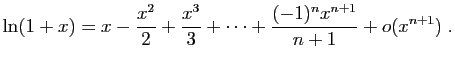
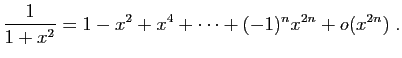
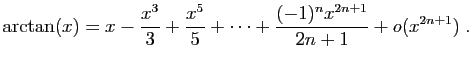
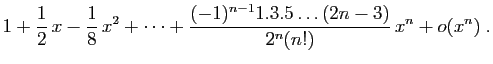
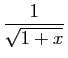
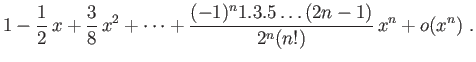
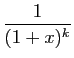
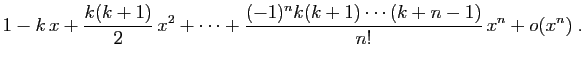
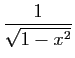
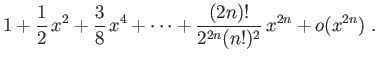
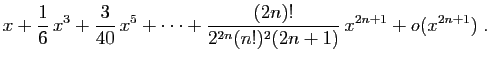
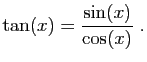
![]() et
et ![]() à
l'ordre
à
l'ordre ![]() :
:
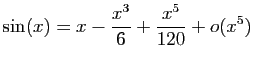 et
et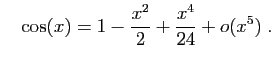
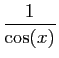
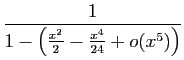
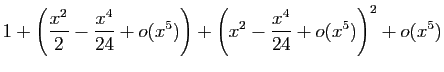
 et
et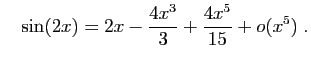
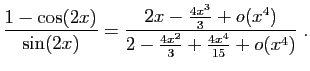
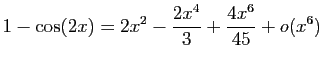 et
et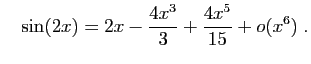
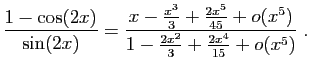
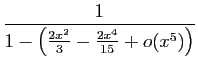
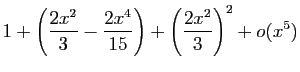
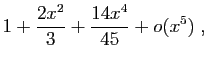
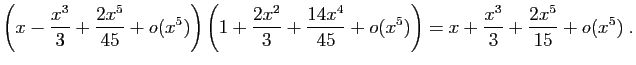
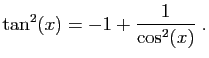
![]() , vous n'obtiendrez
finalement que l'ordre
, vous n'obtiendrez
finalement que l'ordre ![]() .
Les calculs successifs sont les suivants.
.
Les calculs successifs sont les suivants.
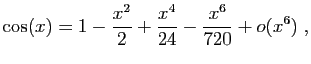
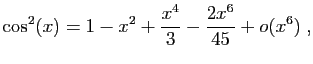
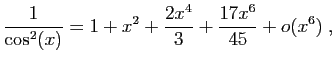
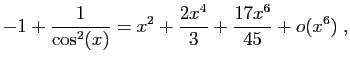
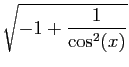
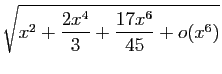
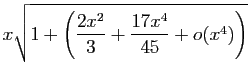
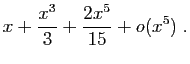
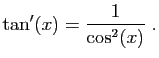
![]() pour la dérivée (ce qui en
l'occurrence ne change pas grand-chose).
pour la dérivée (ce qui en
l'occurrence ne change pas grand-chose).
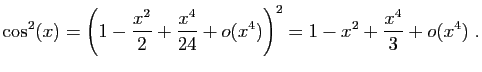
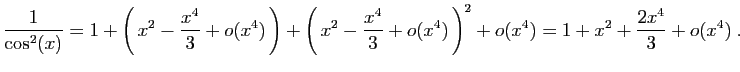
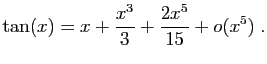
![]() .
.
![]() est
de la forme
est
de la forme
![]() , où
, où ![]() ,
, ![]() et
et ![]() sont des
réels à déterminer. Alors :
sont des
réels à déterminer. Alors :
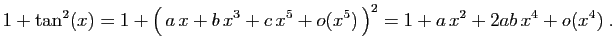
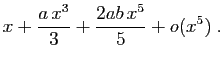
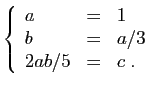
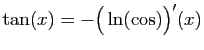 .
.
![]() .
.
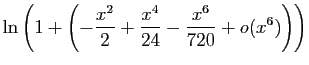
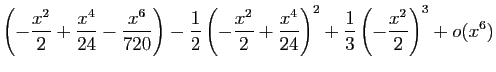
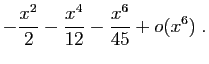
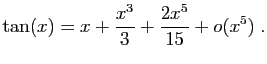
![]() .
.
![]() d'ordre
d'ordre ![]() :
:
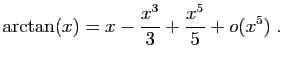
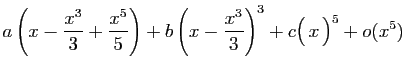
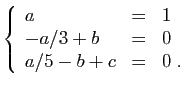
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales