- somme :
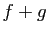 admet un développement limité en 0,
dont le polynôme de Taylor est la somme de ceux de
admet un développement limité en 0,
dont le polynôme de Taylor est la somme de ceux de 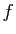 et
et 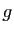 .
.
- produit :
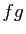 admet un développement limité en 0,
dont le polynôme de Taylor est constitué des termes de degrés
inférieurs ou égaux à
admet un développement limité en 0,
dont le polynôme de Taylor est constitué des termes de degrés
inférieurs ou égaux à 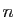 dans le produit
dans le produit 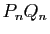 .
.
- composition : si
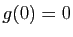 , alors
, alors
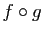 admet un développement limité en 0,
dont le polynôme de Taylor est constitué des termes de degrés
inférieurs ou égaux à
admet un développement limité en 0,
dont le polynôme de Taylor est constitué des termes de degrés
inférieurs ou égaux à 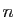 dans le polynôme composé
dans le polynôme composé
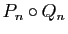 .
.
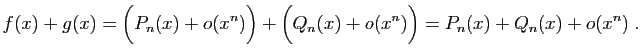
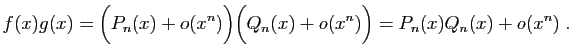
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales