On trouve dans les développements limités une idée simple, qui
est l'idée de base de toute approximation : pour
approcher une fonction au voisinage d'un point, il faut choisir une
échelle «d'infiniment petits»(les 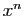 dans le cas des
développements ordinaires). On écrit alors l'approximation
souhaitée comme une combinaison linéaire des infiniment petits de
l'échelle. Bien d'autres échelles que les
dans le cas des
développements ordinaires). On écrit alors l'approximation
souhaitée comme une combinaison linéaire des infiniment petits de
l'échelle. Bien d'autres échelles que les 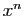 sont possibles. On
peut aussi transposer la même idée pour des développements au
voisinage de
sont possibles. On
peut aussi transposer la même idée pour des développements au
voisinage de 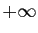 , ou encore pour des échelles d'infiniment
grands. Nous ne ferons pas de théorie générale des
développement asymptotiques dans cette section. Nous nous
contenterons d'une liste d'exemples, qui se déduisent tous
par composition
des développement limités ordinaires. Cette liste est loin
d'être exhaustive, mais vous donnera une idée du type de
généralisations que l'on peut donner aux polynômes de Taylor.
Reprendre vous-même les calculs est un exercice conseillé...
, ou encore pour des échelles d'infiniment
grands. Nous ne ferons pas de théorie générale des
développement asymptotiques dans cette section. Nous nous
contenterons d'une liste d'exemples, qui se déduisent tous
par composition
des développement limités ordinaires. Cette liste est loin
d'être exhaustive, mais vous donnera une idée du type de
généralisations que l'on peut donner aux polynômes de Taylor.
Reprendre vous-même les calculs est un exercice conseillé...
Échelle des 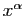 au voisinage de
au voisinage de 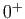
Échelle des
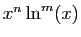 au voisinage de
au voisinage de 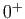
Échelle des 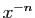 au voisinage de
au voisinage de 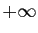
Échelle des
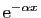 au voisinage de
au voisinage de 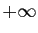
Échelle des 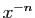 au voisinage de
au voisinage de 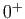
Échelle des
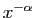 au voisinage de
au voisinage de 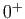
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() au voisinage de
au voisinage de ![]()
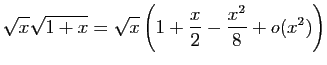
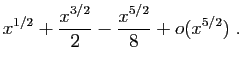
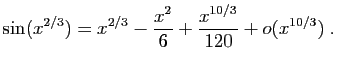
![]() au voisinage de
au voisinage de ![]()
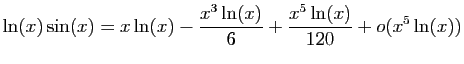
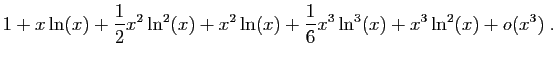
![]() au voisinage de
au voisinage de ![]()
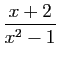
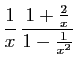
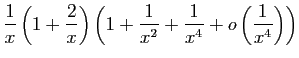
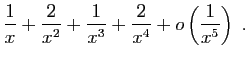

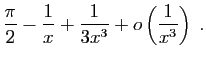
![]() au voisinage de
au voisinage de ![]()
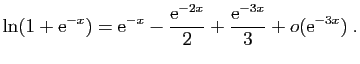
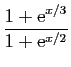
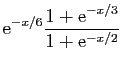
![]() au voisinage de
au voisinage de ![]()
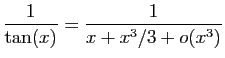
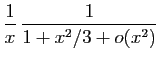
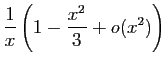
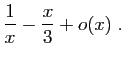
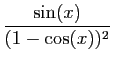
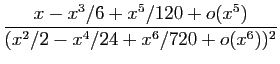
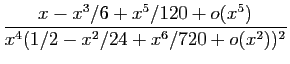
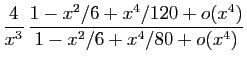
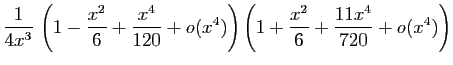
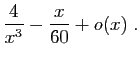
![]() au voisinage de
au voisinage de ![]()
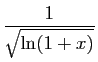
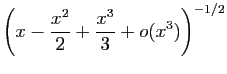
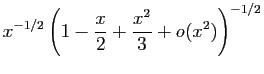
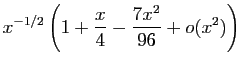
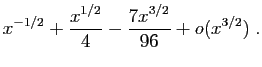
![$\displaystyle \frac{\sqrt[3]{\ln(1+x)}}{\sqrt{\sin^3(x)}}$](img288.gif)
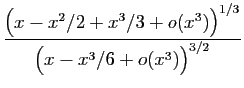
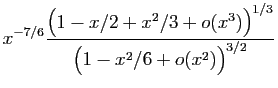
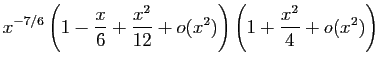
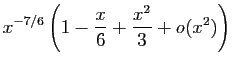
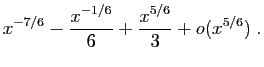
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales