Madhava de Sangamagramma

Madhava de Sangamagramma (1350-1425) est né près de Cochin, sur la côte sud-ouest de l'Inde, dans l'état de Kerala. L'ampleur de ses contributions mathématiques n'a été mise en lumière que récemment. Il semble qu'il soit le premier au monde a avoir systématisé les passages à la limite, à partir des procédures finies des mathématiques de l'antiquité : c'est ce qui constitue de nos jours le fondement de l'analyse telle qu'elle vous est enseignée.

Tous les travaux mathématiques de Madhava ont été perdus, et ses découvertes ne sont connues que par les écrits de mathématiciens indiens plus récents, en particulier Jyesthadeva (1500-1575). Dans un livre paru en 1530, ce dernier décrit le développement de arc tangente obtenu par Madhava vers 1400, soit plus de deux siècles avant Newton et Gregory.

Le premier terme est le produit du sinus donné et du rayon de l'arc désiré, divisé par le cosinus de l'arc. Les termes suivants sont obtenus par un procédé d'itération, quand le premier terme est multiplié de façon répétée par le carré du sinus et divisé par le carré du cosinus. Tous les termes sont ensuite divisés par les nombres impairs 1, 3, 5,... L'arc est obtenu en ajoutant et soustrayant respectivement les termes de rang impair et ceux de rang pair.

Vous avez du mal a reconnaître le développement de $\arctan(x)$ ? C'est un peu normal. Le texte donne la recette pour trouver un angle $\theta$ dont le sinus et le cosinus sont connus. En substance il faut commencer par calculer le rapport $x=\sin(\theta)/\cos(\theta)$ , c'est-à-dire la tangente. Ensuite, il faut multiplier de façon répétée ce rapport par son carré (donc calculer $x, x^3, x^5,\ldots$ ) Puis les termes doivent être divisés par les entiers impairs (soit $x, x^3/3, x^5/5\ldots$ Il reste à ajouter en alternant les signes :

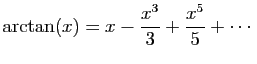
$\displaystyle \arctan(x) = x-\frac{x^3}{3}+\frac{x^5}{5}+\cdots$