Il convient tout d'abord de définir ce que l'on entend par «
critère d'approximation». Considérons une fonction ![]() ,
supposée continue sur un intervalle
,
supposée continue sur un intervalle ![]() . Si l'on désire
l'approcher par un polynôme
. Si l'on désire
l'approcher par un polynôme ![]() , le plus intuitif est sans
doute de considérer l'erreur d'approximation maximale sur tout
l'intervalle. On la note (pour des raisons que vous apprendrez plus
tard)
, le plus intuitif est sans
doute de considérer l'erreur d'approximation maximale sur tout
l'intervalle. On la note (pour des raisons que vous apprendrez plus
tard)
![]() .
.
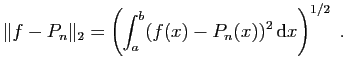
Sur ![]() , les polynômes de meilleure approximation s'expriment
sur la base des polynômes de Legendre.
On peut définir le polynôme de Legendre (normalisé) de degré
, les polynômes de meilleure approximation s'expriment
sur la base des polynômes de Legendre.
On peut définir le polynôme de Legendre (normalisé) de degré ![]() par la formule suivante.
par la formule suivante.
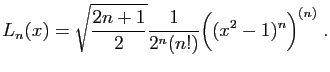
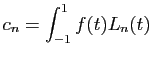
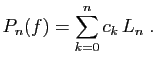
Voici une expérience. Prenons pour ![]() la fonction exponentielle,
sur l'intervalle
la fonction exponentielle,
sur l'intervalle ![]() . Pour
. Pour ![]() allant de
allant de ![]() à
à ![]() , nous avons
calculé l'erreur maximale
, nous avons
calculé l'erreur maximale
![]() , en prenant pour
, en prenant pour ![]() le
polynôme de Taylor de degré
le
polynôme de Taylor de degré ![]() en 0, puis le polynôme
d'approximation de Legendre de même degré. Les résultats sont
donnés dans le tableau ci-dessous : Legendre l'emporte haut la main !
en 0, puis le polynôme
d'approximation de Legendre de même degré. Les résultats sont
donnés dans le tableau ci-dessous : Legendre l'emporte haut la main !
| Taylor |
|
|
|
|
|
|
| Legendre |
|
|
|
|
|
|
Lorsque nous perdons un de nos confrères les plus avancés en âge, nos regrets sont adoucis par la pensée qu'il a moins souffert à ses derniers moments, et qu'affaibli par les années, il s'est éteint sans douleur. Cette consolation nous manque aujourd'hui : la maladie qui a terminé les jours de M. Legendre dans sa 81e année, a été longue et douloureuse ; mais il en a supporté les souffrances avec courage et sans se faire illusion sur leur fatale issue ; avec une résignation que devaient lui rendre bien difficile, le bonheur qu'il trouvait dans son intérieur, et les soins et les vux dont il était entouré.
Notre confrère a souvent exprimé le désir qu'en parlant de lui, il ne fût question que de ses travaux, qui sont, en effet, toute sa vie. Je me conformerai religieusement à sa volonté, dans cet hommage que je viens rendre, au nom de l'Académie des Sciences et du Bureau des Longitudes, au géomètre illustre, au doyen de la science, dont le monde savant va pleurer la perte.Nous aussi, nous respecterons sa volonté : pour une fois, vous serez privés de ces ragots dont nous vous savons friands.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales