D'après le théorème 2,
un sous-espace vectoriel contient toutes les combinaisons
linéaires d'un nombre quelconque de vecteurs : pour tout entier  ,
pour tous vecteurs
,
pour tous vecteurs
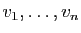 de
de  , et pour tous réels
, et pour tous réels
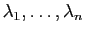 ,
,
Une des manières de fabriquer un sous-espace vectoriel est de partir
d'un ensemble quelconque d'éléments, puis de lui ajouter toutes les
combinaisons linéaires de ces éléments.
Définition 4
Soit  un espace vectoriel et
un espace vectoriel et 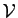 un ensemble non vide
(fini ou non) de
vecteurs de
un ensemble non vide
(fini ou non) de
vecteurs de  . On appelle sous-espace engendré par
. On appelle sous-espace engendré par 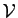 l'ensemble des combinaisons linéaires d'un nombre fini quelconque
d'éléments de
l'ensemble des combinaisons linéaires d'un nombre fini quelconque
d'éléments de 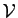 .
.
L'ensemble des combinaisons linéaires
d'éléments de 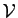 est un espace vectoriel, d'après le
théorème 2. Le même théorème implique
aussi que tout espace vectoriel contenant
est un espace vectoriel, d'après le
théorème 2. Le même théorème implique
aussi que tout espace vectoriel contenant 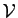 doit contenir
toutes les combinaisons linéaires de ses éléments. Donc le
sous-espace engendré par
doit contenir
toutes les combinaisons linéaires de ses éléments. Donc le
sous-espace engendré par 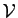 est inclus dans tout sous-espace
contenant
est inclus dans tout sous-espace
contenant 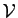 .
Une famille finie de vecteurs est un
.
Une famille finie de vecteurs est un  -uplet de vecteurs.
-uplet de vecteurs.
L'espace vectoriel engendré par 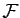 est l'ensemble
des combinaisons linéaires de
est l'ensemble
des combinaisons linéaires de
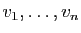 .
.
À cause de la commutativité de l'addition, changer l'ordre
dans lequel on écrit les vecteurs de la famille, ne modifie pas
l'espace engendré.
Pour 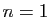 , l'espace engendré par un seul vecteur
, l'espace engendré par un seul vecteur  (non nul) est une
droite vectorielle :
(non nul) est une
droite vectorielle :
Pour 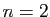 , l'espace engendré par deux vecteurs
, l'espace engendré par deux vecteurs  et
et 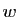 (non
proportionnels) est un plan vectoriel :
(non
proportionnels) est un plan vectoriel :
L'espace vectoriel
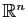 est engendré par les
est engendré par les
 vecteurs
vecteurs
En effet, on peut écrire tout vecteur
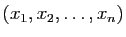 de
de
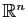 , comme la combinaison linéaire :
, comme la combinaison linéaire :
Deux familles de vecteurs différentes peuvent engendrer le même
espace vectoriel. Par exemple
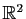 est engendré par
est engendré par
mais aussi par
En effet, tout vecteur 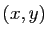 s'écrit :
s'écrit :
Définition 5
Soit  un espace vectoriel et
un espace vectoriel et 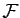 une famille d'éléments de
une famille d'éléments de
 . On dit que
. On dit que 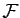 est une famille génératrice si l'espace
engendré par
est une famille génératrice si l'espace
engendré par 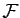 est égal à
est égal à  .
.
Par exemple
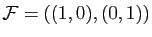 et
et
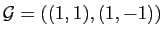 sont deux
familles génératrices de
sont deux
familles génératrices de
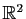 .
Par contre
.
Par contre
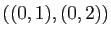 n'est pas une famille génératrice de
n'est pas une famille génératrice de
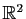 .
.
Les familles suivantes sont aussi
des familles génératrices de
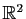 .
.
Par rapport à 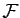 et
et 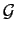 , elles contiennent des vecteurs
superflus. Si dans une famille de vecteurs, un vecteur est
combinaison linéaire des autres, on peut l'enlever de la
famille sans changer l'espace engendré. Une famille de laquelle on
ne peut rien enlever sans changer l'espace engendré est une famille
libre.
, elles contiennent des vecteurs
superflus. Si dans une famille de vecteurs, un vecteur est
combinaison linéaire des autres, on peut l'enlever de la
famille sans changer l'espace engendré. Une famille de laquelle on
ne peut rien enlever sans changer l'espace engendré est une famille
libre.
Définition 6
Soit
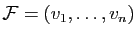 une famille finie de vecteurs. On dit que
une famille finie de vecteurs. On dit que
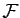 est une famille libre si pour tous
est une famille libre si pour tous
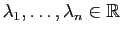 ,
,
Elle est dite liée dans le cas contraire.
On dit aussi que les vecteurs
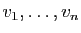 sont
linéairement indépendants quand leur famille est libre.
Comme cas particuliers, une famille contenant le vecteur nul
est liée ; une famille contenant un seul
vecteur non nul est libre.
On utilise souvent la caractérisation suivante :
sont
linéairement indépendants quand leur famille est libre.
Comme cas particuliers, une famille contenant le vecteur nul
est liée ; une famille contenant un seul
vecteur non nul est libre.
On utilise souvent la caractérisation suivante :
Proposition 3
Soit  un entier au moins égal à
un entier au moins égal à 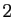 .
Une famille de
.
Une famille de  vecteurs est liée si et seulement
si l'un des vecteurs est combinaison
linéaire des autres.
vecteurs est liée si et seulement
si l'un des vecteurs est combinaison
linéaire des autres.
Démonstration : Soit
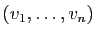 une famille liée. Par définition, il
existe une combinaison linéaire nulle, dont les coefficients ne sont
pas tous nuls.
une famille liée. Par définition, il
existe une combinaison linéaire nulle, dont les coefficients ne sont
pas tous nuls.
et au moins un des 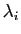 est non nul.
Observons que la propriété pour une famille d'être libre ou
liée ne dépend pas de l'ordre dans lequel on écrit les
vecteurs. Sans perte de généralité nous pouvons supposer que
est non nul.
Observons que la propriété pour une famille d'être libre ou
liée ne dépend pas de l'ordre dans lequel on écrit les
vecteurs. Sans perte de généralité nous pouvons supposer que
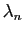 est non nul. On en déduit alors :
est non nul. On en déduit alors :
Réciproquement, supposons que 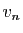 soit combinaison linéaire de
soit combinaison linéaire de
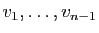 :
:
Alors :
Donc la famille
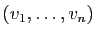 est liée.
est liée.
Dans
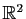 ,
la famille
,
la famille
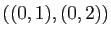 est liée.
A l'inverse, les familles
est liée.
A l'inverse, les familles
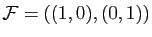 et
et
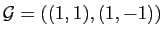 sont deux familles libres de
sont deux familles libres de
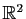 .
Dans
.
Dans
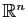 ,
,
est une famille libre.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
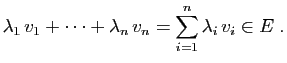
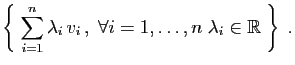
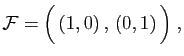
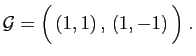
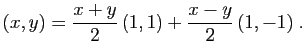
![]() .
.
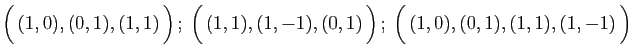
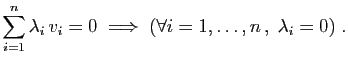
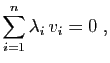
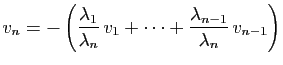
![]() ,
la famille
,
la famille
![]() est liée.
A l'inverse, les familles
est liée.
A l'inverse, les familles
![]() et
et
![]() sont deux familles libres de
sont deux familles libres de
![]() .
Dans
.
Dans
![]() ,
,
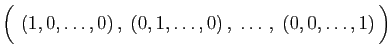
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales