Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours :
Soient  et
et 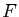 deux espaces vectoriels et
deux espaces vectoriels et 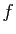 une application de
une application de  dans
dans 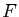 . Soit
. Soit 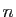 un entier strictement positif, et
un entier strictement positif, et
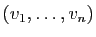 une famille de vecteurs de
une famille de vecteurs de  .
.
- On suppose que
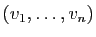 est génératrice. Soit
est génératrice. Soit 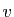 un
vecteur quelconque de
un
vecteur quelconque de  . Montrer que la famille
. Montrer que la famille
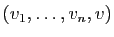 est génératrice.
est génératrice.
- On suppose que
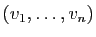 est libre. Montrer que la
famille
est libre. Montrer que la
famille
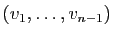 est libre.
est libre.
- On suppose que
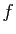 est surjective et que
est surjective et que
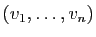 est
génératrice dans
est
génératrice dans  . Montrer que
. Montrer que
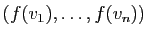 est
génératrice dans
est
génératrice dans 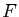 .
.
- On suppose que
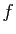 est injective et que
est injective et que
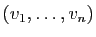 est
libre dans
est
libre dans  . Montrer que
. Montrer que
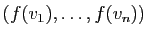 est
libre dans
est
libre dans 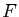 .
.
- On suppose que
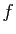 est bijective. Montrer que
est bijective. Montrer que
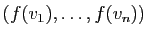 est une base de
est une base de 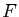 si et seulement si
si et seulement si
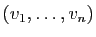 est une base de
est une base de  .
.
Exercice :
Soient 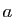 et
et 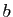 deux réels. On considère les
trois vecteurs de
deux réels. On considère les
trois vecteurs de
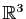 suivants.
suivants.
On note :
-
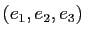 la base canonique de
la base canonique de
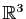 :
:
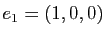 ,
,
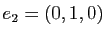 ,
,
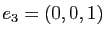 .
.
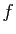 l'application linéaire de
l'application linéaire de
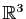 dans
dans
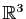 qui à
qui à 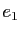 associe
associe 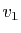 , à
, à 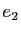 associe
associe 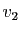 et à
et à 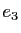 associe
associe 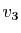 .
.
- Montrer que
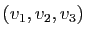 est une base de
est une base de
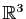 si et seulement si
si et seulement si
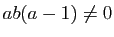 .
.
- Écrire en fonction de
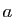 et
et 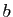 la matrice de
la matrice de 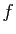 dans la base
canonique
dans la base
canonique
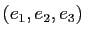 .
.
- Pour
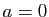 , montrer que les deux vecteurs
, montrer que les deux vecteurs 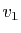 et
et 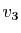 forment une
famille libre.
forment une
famille libre.
- Pour
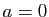 , montrer que le noyau de
, montrer que le noyau de 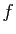 est la droite vectorielle
engendrée par
est la droite vectorielle
engendrée par 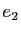 .
.
- Pour
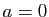 , donner une base de
, donner une base de
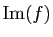 .
.
- Pour
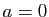 , vérifier que
, vérifier que
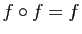 .
.
- Pour
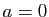 , montrer que
, montrer que
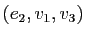 est une base de
est une base de
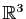 . Écrire la matrice de
. Écrire la matrice de 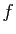 dans la base
dans la base
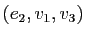 .
.
- Pour
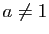 et
et 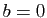 ,
montrer que
,
montrer que
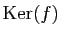 est une droite vectorielle,
dont on donnera un vecteur directeur fonction de
est une droite vectorielle,
dont on donnera un vecteur directeur fonction de 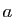 .
.
- Pour
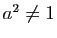 et
et 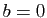 ,
montrer que
,
montrer que
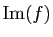 est le plan vectoriel
engendré par
est le plan vectoriel
engendré par 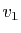 et
et 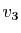 .
.
- Pour
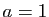 et
et 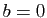 , donner une base de
, donner une base de
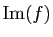 et une base de
et une base de
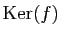 .
.
- Pour
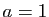 et
et 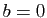 ,
vérifier que la réunion des deux bases de la question
précédente forme une base de
,
vérifier que la réunion des deux bases de la question
précédente forme une base de
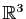 et donner la matrice de
et donner la matrice de 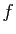 dans cette nouvelle base.
dans cette nouvelle base.
- Pour
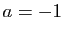 ,
, 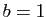 , montrer que l'application
, montrer que l'application 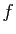 est bijective.
est bijective.
- On considère l'application
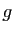 qui à
qui à 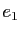 associe
associe 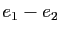 , à
, à
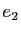 associe
associe
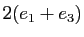 , et à
, et à 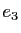 associe
associe 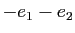 . Ecrire la
matrice de
. Ecrire la
matrice de 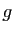 dans la base
dans la base
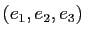 .
.
- Pour
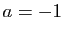 ,
, 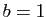 , écrire la matrice de l'application
, écrire la matrice de l'application 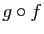 .
En déduire la matrice de l'application réciproque
.
En déduire la matrice de l'application réciproque 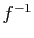 dans la
base
dans la
base
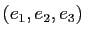 .
.
- Pour
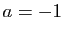 ,
, 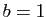 , donner la matrice de l'application
, donner la matrice de l'application 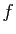 dans la
base
dans la
base
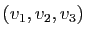 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() et
et ![]() deux espaces vectoriels et
deux espaces vectoriels et ![]() une application de
une application de ![]() dans
dans ![]() . Soit
. Soit ![]() un entier strictement positif, et
un entier strictement positif, et
![]() une famille de vecteurs de
une famille de vecteurs de ![]() .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales