Montrons maintenant la réciproque. Si ![]() est bijective,
l'application réciproque
est bijective,
l'application réciproque ![]() est elle aussi linéaire et
bijective. Si
est elle aussi linéaire et
bijective. Si
![]() est une base de
est une base de ![]() , alors
, alors
![]() est une base
de
est une base
de ![]() , en appliquant ce qui précède à
, en appliquant ce qui précède à ![]() .
.
Questions de cours :
Montrons maintenant la réciproque. Si ![]() est bijective,
l'application réciproque
est bijective,
l'application réciproque ![]() est elle aussi linéaire et
bijective. Si
est elle aussi linéaire et
bijective. Si
![]() est une base de
est une base de ![]() , alors
, alors
![]() est une base
de
est une base
de ![]() , en appliquant ce qui précède à
, en appliquant ce qui précède à ![]() .
.
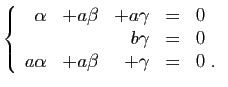
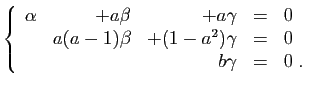
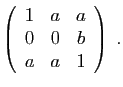
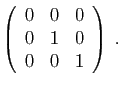
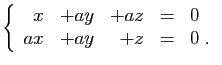
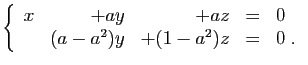
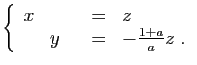
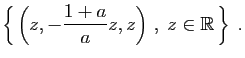
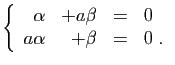
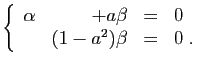
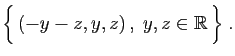
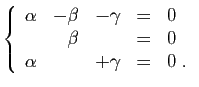
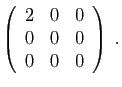
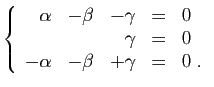
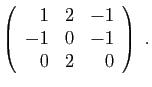
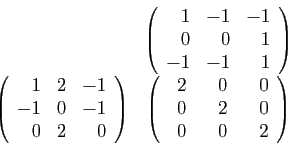
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales