Soit 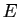 un espace vectoriel de dimension
un espace vectoriel de dimension 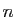 , et
, et 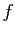 un endomorphisme
(application linéaire de
un endomorphisme
(application linéaire de 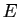 dans
dans 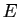 ). Le déterminant dans une
base de
). Le déterminant dans une
base de 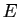 de l'image
par
de l'image
par 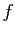 de cette même base, ne dépend pas de la
base choisie.
de cette même base, ne dépend pas de la
base choisie.
Démonstration : L'application qui à un 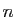 -uplet de vecteurs
-uplet de vecteurs
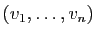 associe
associe
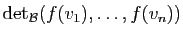 est
est 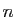 -linéaire
et alternée. D'après le théorème 2, elle
est proportionnelle à l'application
-linéaire
et alternée. D'après le théorème 2, elle
est proportionnelle à l'application
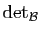 . Il existe
donc une constante
. Il existe
donc une constante 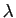 telle que
telle que
Or par définition :
En utilisant le cas particulier où les vecteurs
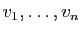 sont
ceux de la base
sont
ceux de la base 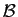 , la constante
, la constante 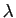 est
nécessairement
est
nécessairement
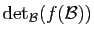 .
De même,
.
De même,
Mais d'après la proposition 4,
Donc
Mais aussi :
Il s'ensuit que
 La proposition 8 permet de définir le
déterminant d'un endomorphisme.
La proposition 8 permet de définir le
déterminant d'un endomorphisme.
Définition 7
On appelle déterminant de l'endomorphisme 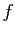 , et on note
, et on note
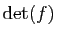 la valeur de
la valeur de
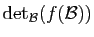 , commune à toutes les bases
, commune à toutes les bases 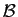 .
.
Le déterminant de 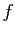 est donc égal au déterminant de la
matrice de
est donc égal au déterminant de la
matrice de 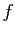 dans n'importe quelle base.
De plus, si
dans n'importe quelle base.
De plus, si 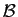 est une base de
est une base de 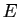 et
et
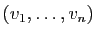 un
un
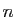 -uplet quelconque de vecteurs de
-uplet quelconque de vecteurs de 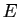 :
:
Théorème 3
Soient 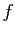 et
et 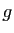 deux endomorphismes de
deux endomorphismes de 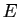 . Alors :
. Alors :
Démonstration : Soit 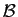 une base de
une base de 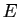 . Par définition du déterminant
d'un endomorphisme,
. Par définition du déterminant
d'un endomorphisme,
 Dans le cas particulier où
Dans le cas particulier où 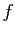 est un automorphisme de
est un automorphisme de 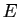 , son
déterminant est non nul (l'image par
, son
déterminant est non nul (l'image par 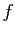 d'une base est une
base). Sa composée avec l'application réciproque
d'une base est une
base). Sa composée avec l'application réciproque 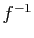 est
l'identité, de déterminant
est
l'identité, de déterminant 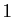 . Donc :
. Donc :
La traduction en termes de matrices est la suivante.
Corollaire 2
- Soient
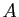 et
et 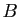 deux matrices de taille
deux matrices de taille 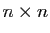 .
.
- Une matrice carrée
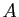 est inversible si et seulement si son
déterminant est non nul, et alors :
est inversible si et seulement si son
déterminant est non nul, et alors :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
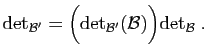
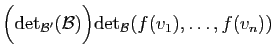
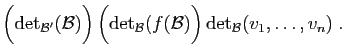

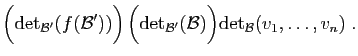
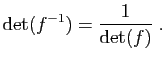
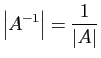
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales