Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours : Soit 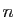 un entier et
un entier et
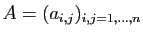 une matrice de
taille
une matrice de
taille 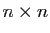 .
.
- Donner l'expression du déterminant de
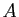 en fonction de ses coefficients.
en fonction de ses coefficients.
- Démontrer que le déterminant de la transposée de
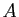 est égal
au déterminant de
est égal
au déterminant de 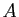 .
.
- Donner la définition des cofacteurs de
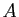 .
.
- Soit
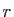 un entier tel que
un entier tel que
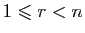 .
Démontrer que si le rang de
.
Démontrer que si le rang de 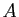 est strictement inférieur à
est strictement inférieur à 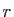 alors tous les mineurs d'ordre
alors tous les mineurs d'ordre 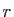 de
de 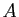 sont nuls.
sont nuls.
- Démontrer que si le rang de
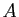 est supérieur ou égal à
est supérieur ou égal à 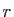 alors il existe un mineur d'ordre
alors il existe un mineur d'ordre 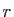 non nul.
non nul.
Exercice 1 :Soit
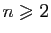 un entier. Soient
un entier. Soient
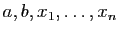 des
réels. On note
des
réels. On note 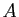 la matrice de taille
la matrice de taille 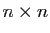 dont la diagonale
est
dont la diagonale
est
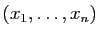 , les termes au-dessus sont tous égaux à
, les termes au-dessus sont tous égaux à
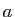 , les termes au-dessous tous égaux à
, les termes au-dessous tous égaux à 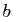 .
.
- Dans le cas particulier où
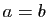 et tous les
et tous les 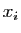 sont égaux à
sont égaux à
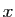 , montrer que
, montrer que
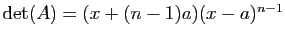 .
.
- On note
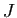 la matrice de taille
la matrice de taille 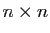 dont tous les
coefficients valent
dont tous les
coefficients valent 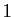 . Dans le cas général,
montrer que le polynôme
. Dans le cas général,
montrer que le polynôme
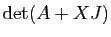 est de degré
est de degré 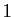 en
en
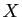 .
.
- Calculer
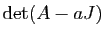 et
et
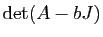 .
.
- On suppose
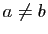 .
Montrer que
.
Montrer que
où 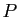 désigne le polynôme
désigne le polynôme
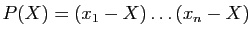 .
.
- En déduire que pour
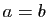 ,
,
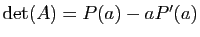 .
.
Exercice 2 :Soit
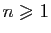 un entier.
Soient
un entier.
Soient
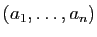 et
et
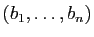 deux éléments de
deux éléments de
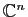 tels que
tels que
On appelle matrice de Cauchy et on note 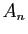 la
matrice de taille
la
matrice de taille 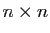 dont le coefficient d'indices
dont le coefficient d'indices 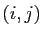 est
est
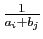 . On note
. On note 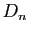 son déterminant.
son déterminant.
- Montrer que si
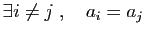
ou
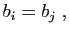
alors 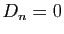 .
.
- Montrer que
- Montrer que
- Montrer que
- Montrer que
- Montrer que
- En déduire que
- On note
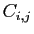 le cofacteur d'indices
le cofacteur d'indices 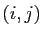 de la matrice
de la matrice 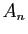 .
On suppose que
.
On suppose que 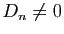 .
Montrer que
.
Montrer que
- La matrice de Hilbert est le cas particulier de matrice Cauchy
obtenu pour
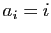 et
et 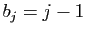 . Pour
. Pour 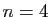 , écrire la matrice de
Hilbert et calculer son déterminant.
, écrire la matrice de
Hilbert et calculer son déterminant.
- Calculer l'inverse de la matrice de Hilbert pour
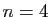 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() un entier et
un entier et
![]() une matrice de
taille
une matrice de
taille ![]() .
.

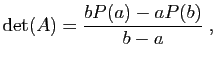
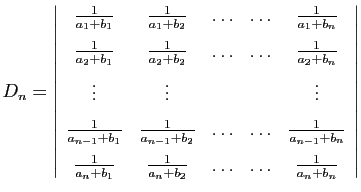
![$\displaystyle D_n=\frac{1}{(a_n+b_1)\cdots(a_n+b_n)}
\left\vert\begin{array}{cc...
...rac{a_n+b_n}{a_{n-1}+b_n} [1.5ex]
1&1&\ldots&\ldots&1
\end{array}\right\vert
$](img563.gif)
![$\displaystyle D_n=\frac{1}{(a_n+b_1)\cdots(a_n+b_n)}
\left\vert\begin{array}{cc...
...a_n-a_{n-1}}{a_{n-1}+b_n} [1.5ex]
1&1&\ldots&\ldots&1
\end{array}\right\vert
$](img564.gif)
![$\displaystyle D_n=\frac{(a_n-a_1)\cdots(a_n-a_{n-1})}{(a_n+b_1)\cdots(a_n+b_n)}...
...ots&\frac{1}{a_{n-1}+b_n} [1.5ex]
1&1&\ldots&\ldots&1
\end{array}\right\vert
$](img565.gif)
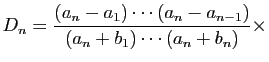
![$\displaystyle \left\vert\begin{array}{ccccc}
\frac{b_n-b_1}{(a_1+b_1)(a_1+b_n)}...
...1}+b_n)}&\frac{1}{a_{n-1}+b_n} [1.5ex]
0&0&\ldots&0&1
\end{array}\right\vert
$](img567.gif)
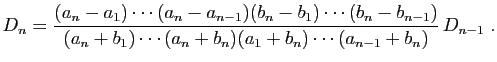
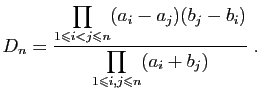
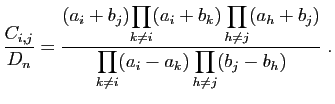
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales