- Écrire toutes les permutations de
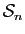
- Écrire la décomposition en orbites de chaque permutation
- En déduire une décomposition en produit de cycles, puis en produit de permutations.
- Calculer la signature.
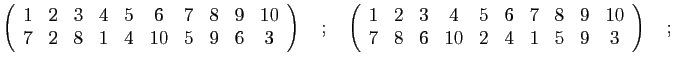
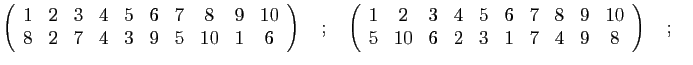
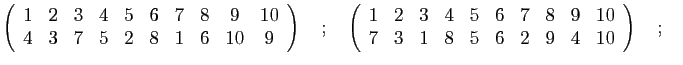
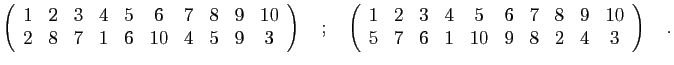
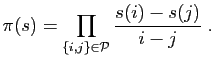
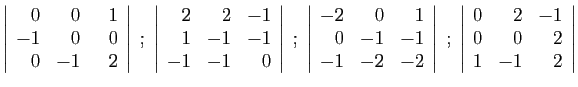
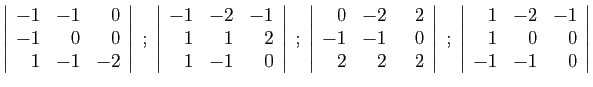
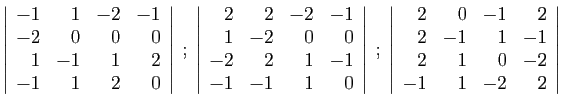
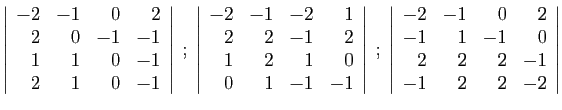
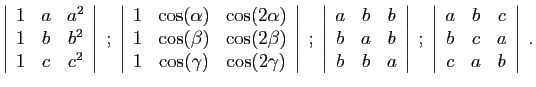
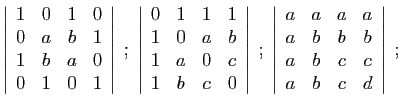
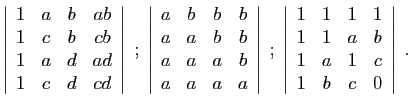
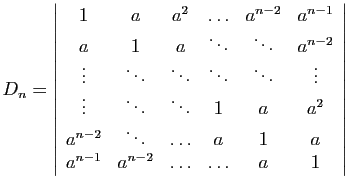


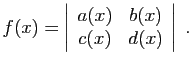
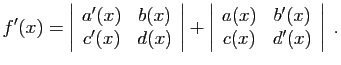
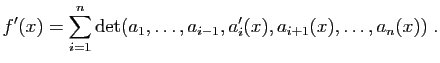
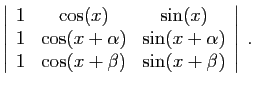
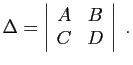
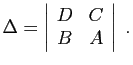
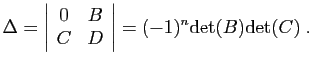
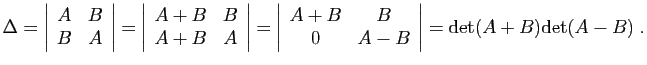
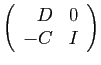 .
.
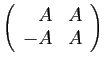 est-elle inversible ? Si c'est le cas, quel est son inverse ?
est-elle inversible ? Si c'est le cas, quel est son inverse ?
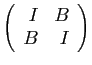 est-elle inversible ? Si c'est le cas, quel est son inverse ?
est-elle inversible ? Si c'est le cas, quel est son inverse ?
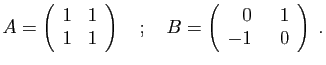
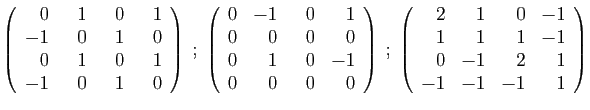

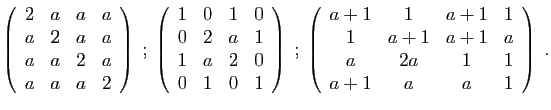
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales