Les résultats de cette section sont à connaître par c ur :
ils vous permettent de calculer les dérivées de toutes les fonctions
que vous rencontrerez, à partir d'un petit nombre de dérivées
usuelles.
ur :
ils vous permettent de calculer les dérivées de toutes les fonctions
que vous rencontrerez, à partir d'un petit nombre de dérivées
usuelles.
Théorème 1
Soient  et
et 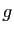 deux fonctions définies sur un intervalle
deux fonctions définies sur un intervalle  contenant
contenant  . On suppose que
. On suppose que  et
et 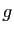 sont dérivables en
sont dérivables en
 . Alors :
. Alors :
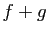 est dérivable en
est dérivable en  , de dérivée
, de dérivée
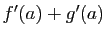
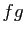 est dérivable en
est dérivable en  , de dérivée
, de dérivée
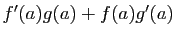 .
.
Comme cas particulier du point 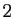 , si
, si 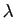 est une constante, la
dérivée de
est une constante, la
dérivée de 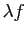 est
est
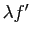 .
Démonstration : Par hypothèse,
.
Démonstration : Par hypothèse,
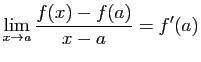
et
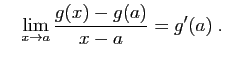
- Écrivons le taux d'accroissement de la somme.
Comme la limite de la somme est la somme des limites, le résultat
s'ensuit.
- Écrivons le taux d'accroissement du produit.
Comme 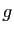 est dérivable, elle est continue en
est dérivable, elle est continue en  , donc
, donc 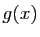 tend
vers
tend
vers 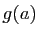 quand
quand 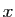 tend vers
tend vers  . La limite d'un produit est le
produit des limites, idem pour la somme. D'où le résultat.
. La limite d'un produit est le
produit des limites, idem pour la somme. D'où le résultat.
 Le théorème 1, combiné avec la
proposition 3, entraîne en particulier que toute
fonction polynôme est dérivable sur
Le théorème 1, combiné avec la
proposition 3, entraîne en particulier que toute
fonction polynôme est dérivable sur
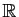 .
.
Démonstration : Par hypothèse, les taux d'accroissement de  en
en  et de
et de 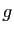 en
en
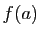 convergent :
convergent :
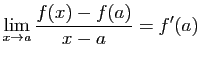
et
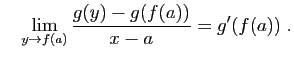
Nous allons utiliser en plus les conséquences suivantes :
- C1 :
 est continue en
est continue en  ,
,
- C2 :
- si
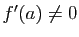 alors
alors
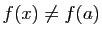 au voisinage de
au voisinage de
 ,
,
- C3 :
- le taux d'accroissement de
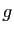 est borné au voisinage de
est borné au voisinage de 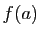 .
.
L'idée consiste à écrire le taux d'accroissement de 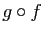 en
en  comme un produit de deux taux :
comme un produit de deux taux :
avec :
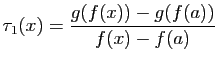
et
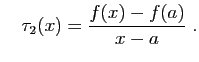
Évidemment, 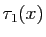 n'est défini que si
n'est défini que si
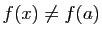 . Mais
si
. Mais
si 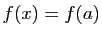 , alors
, alors 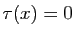 .
.
Considérons d'abord le cas où 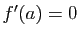 . Dans ce cas,
. Dans ce cas, 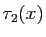 tend vers 0, et comme conséquence de C1 et C3, il existe un
intervalle
tend vers 0, et comme conséquence de C1 et C3, il existe un
intervalle
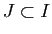 et une constante
et une constante 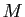 telle que :
telle que :
Donc 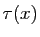 converge vers 0.
converge vers 0.
Considérons maintenant le cas où
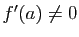 . Comme
conséquence de C2,
. Comme
conséquence de C2, 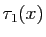 est bien défini au voisinage de
est bien défini au voisinage de
 . La convergence de
. La convergence de 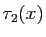 vers
vers 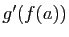 découle de la
dérivabilité de
découle de la
dérivabilité de 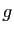 et de la continuité de
et de la continuité de  (composition des
limites).
(composition des
limites). D'après la proposition 3, appliquée à la
fonction inverse
D'après la proposition 3, appliquée à la
fonction inverse
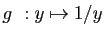 , celle-ci est dérivable en tout
point
, celle-ci est dérivable en tout
point 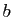 où elle est définie, et
où elle est définie, et
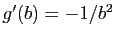 . On déduit du
théorème 2
que si
. On déduit du
théorème 2
que si  est dérivable et ne s'annule pas en
est dérivable et ne s'annule pas en  , alors son
inverse
, alors son
inverse
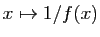 est dérivable, de dérivée
est dérivable, de dérivée
En combinant ceci avec la formule donnant la dérivée d'un produit,
on obtient la dérivée d'un quotient.
Attention à ne pas confondre l'inverse 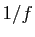 avec la fonction
réciproque
avec la fonction
réciproque 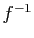 dans le cas où
dans le cas où  est bijective.
est bijective.
Démonstration : Pour tout point 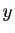 de
de 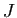 , il existe un unique
, il existe un unique 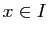 tel que
tel que
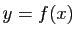 .
Écrivons le taux d'accroissement de
.
Écrivons le taux d'accroissement de 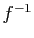 en
en 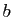 : pour tout
: pour tout
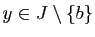 ,
,
Puisque  est continue en
est continue en  ,
, 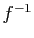 est continue en
est continue en 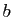 , et donc
, et donc
 Les théorèmes de cette section permettent de démontrer
la dérivabilité de toutes les fonctions que vous aurez
à examiner, à condition d'admettre la dérivabilité
des «briques de base» que sont les fonctions usuelles.
Les théorèmes de cette section permettent de démontrer
la dérivabilité de toutes les fonctions que vous aurez
à examiner, à condition d'admettre la dérivabilité
des «briques de base» que sont les fonctions usuelles.
Toutes les fonctions usuelles sont dérivables en tout
point
d'un intervalle ouvert où elles sont définies.
Ceci concerne les fonctions polynômes, fractions rationnelles,
puissances, exponentielle, logarithme,
sinus, cosinus, mais exclut bien sûr la valeur absolue.
Voici un tableau récapitulatif des
formules de dérivation à connaître par c ur.
ur.
Les dérivées suivantes doivent être connues.
La connaissance des dérivées usuelles, permet, en appliquant la
définition 2, de calculer des limites de taux
d'accroissement.
À titre d'exemple, nous donnons
ci-dessous trois limites à connaître.
Démonstration : Les trois limites sont démontrées dans l'ordre.
- La dérivée de la fonction sinus en 0 est
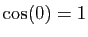 . Son taux
d'accroissement en 0 est :
. Son taux
d'accroissement en 0 est :
D'où le résultat.
- La dérivée de la fonction exponentielle en 0 est
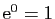 . Son taux
d'accroissement en 0 est :
. Son taux
d'accroissement en 0 est :
D'où le résultat.
- La dérivée de la fonction
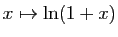 en 0
est
en 0
est 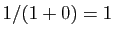 . Son taux
d'accroissement en 0 est :
. Son taux
d'accroissement en 0 est :
D'où le résultat.

 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
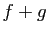 est dérivable en
est dérivable en  , de dérivée
, de dérivée
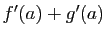
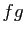 est dérivable en
est dérivable en  , de dérivée
, de dérivée
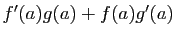 .
.
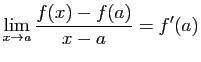 et
et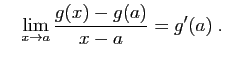
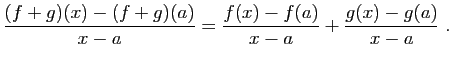
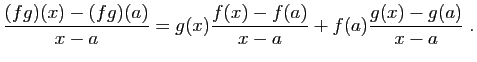
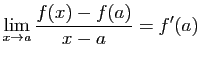 et
et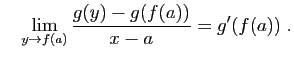
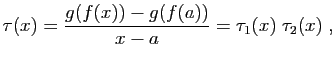
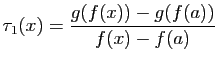 et
et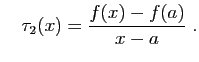
![]() . Dans ce cas,
. Dans ce cas, ![]() tend vers 0, et comme conséquence de C1 et C3, il existe un
intervalle
tend vers 0, et comme conséquence de C1 et C3, il existe un
intervalle
![]() et une constante
et une constante ![]() telle que :
telle que :
![]() . Comme
conséquence de C2,
. Comme
conséquence de C2, ![]() est bien défini au voisinage de
est bien défini au voisinage de
![]() . La convergence de
. La convergence de ![]() vers
vers ![]() découle de la
dérivabilité de
découle de la
dérivabilité de ![]() et de la continuité de
et de la continuité de ![]() (composition des
limites).
(composition des
limites).![]() D'après la proposition 3, appliquée à la
fonction inverse
D'après la proposition 3, appliquée à la
fonction inverse
![]() , celle-ci est dérivable en tout
point
, celle-ci est dérivable en tout
point ![]() où elle est définie, et
où elle est définie, et
![]() . On déduit du
théorème 2
que si
. On déduit du
théorème 2
que si ![]() est dérivable et ne s'annule pas en
est dérivable et ne s'annule pas en ![]() , alors son
inverse
, alors son
inverse
![]() est dérivable, de dérivée
est dérivable, de dérivée
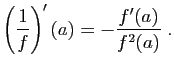
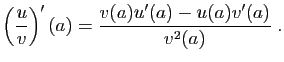
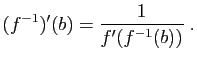
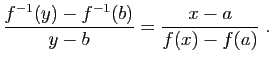
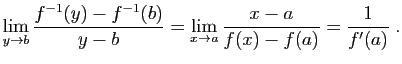
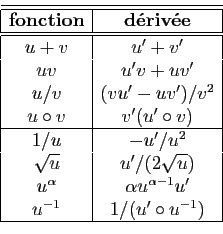
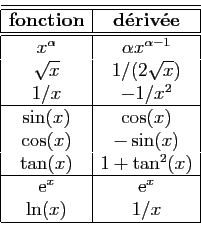
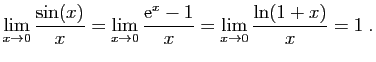
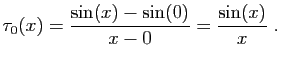
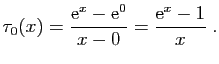
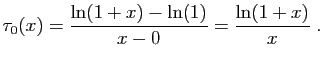
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales