-
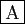
- Le taux d'accroissement
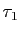 est une fonction de
est une fonction de
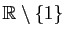 dans
dans
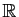 .
.
-
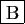
- Le taux d'accroissement
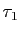 est égal à
est égal à 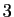 .
.
-
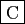
- Pour tout
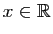 ,
,
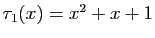 .
.
-
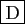
- Le taux d'accroissement
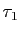 n'admet pas de limite quand
n'admet pas de limite quand 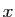 tend vers
tend vers 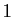 .
.
-
- Le taux d'accroissement
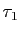 est prolongeable par continuité en
est prolongeable par continuité en 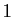 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales