- Donner une expression explicite du taux d'accroissement de
 en un point
en un point  quelconque du domaine de définition.
quelconque du domaine de définition.
- Calculer la limite en
 de ce taux d'accroissement et
retrouver l'expression de la dérivée de
de ce taux d'accroissement et
retrouver l'expression de la dérivée de  en
en  .
.
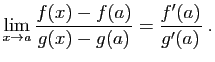
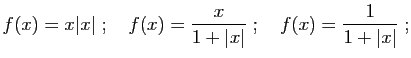
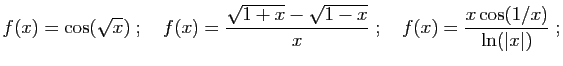
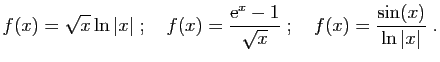
![$\displaystyle f(x)= (x(x-2))^{1/3}
\;;\quad
f(x)= \frac{1}{\sqrt[3]{x^2}}-\frac{1}{\sqrt{x^3}}
\;;\quad
f(x)= \sqrt{x+\sqrt{1+x^2}}\;;
$](img312.gif)
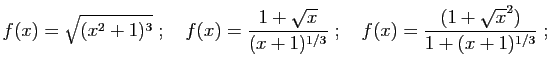
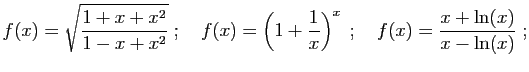
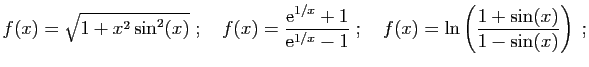
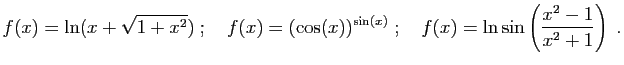
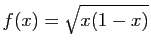 sur
sur ![$\displaystyle [0,1]
\;;\quad
f(x)=\sqrt{(1-x^2)(1-x)}$](img318.gif) sur
sur
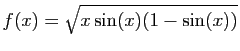 sur
sur
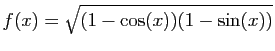 sur
sur
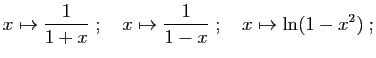
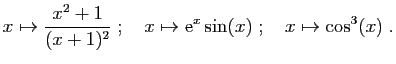
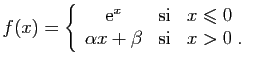
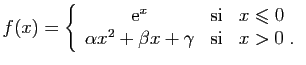
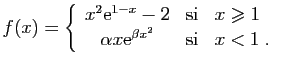
![\begin{displaymath}
h(x)=\left\{
\begin{array}{ccl}
f(x-a)&\mbox{si}&x< a\\
0&\...
...{si}&x\in[a,b]\\
f(x-b)&\mbox{si}& x> b\;.
\end{array}\right.
\end{displaymath}](img347.gif)
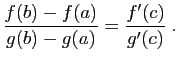
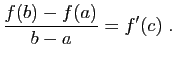
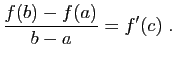
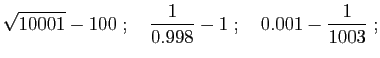
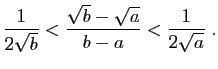
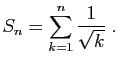
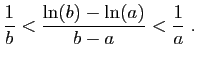
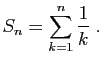
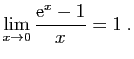
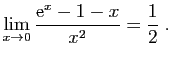
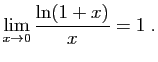
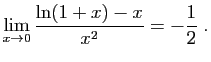
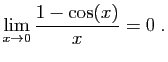
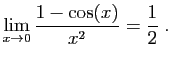
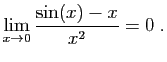
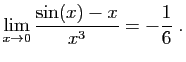
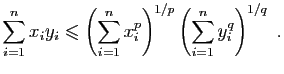
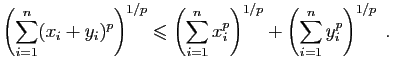
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales