-
 Si
Si 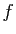 est dérivable en
est dérivable en 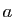 , alors le taux d'accroissement de
, alors le taux d'accroissement de
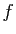 en
en 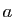 est prolongeable par continuité en
est prolongeable par continuité en 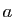 .
.
 Si
Si 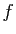 est dérivable en
est dérivable en 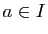 , alors
, alors 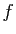 est continue sur un
intervalle ouvert contenant
est continue sur un
intervalle ouvert contenant 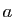 .
.
-
 Si
Si 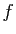 est dérivable sur
est dérivable sur 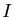 , alors
, alors 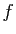 est continue sur
est continue sur 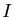 .
.
-
 Si
Si 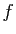 est dérivable à gauche en
est dérivable à gauche en 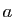 , alors
, alors 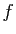 est continue à
gauche en
est continue à
gauche en 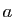 .
.
 Si
Si 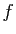 est dérivable à gauche et à droite en
est dérivable à gauche et à droite en 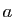 , alors
, alors 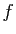 est
dérivable en
est
dérivable en 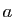 .
.
 Si la dérivée de
Si la dérivée de 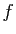 en
en 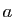 est nulle, alors la tangente à la
courbe représentative de
est nulle, alors la tangente à la
courbe représentative de 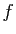 en
en 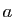 est verticale.
est verticale.
-
 Si la tangente à la courbe représentative de
Si la tangente à la courbe représentative de 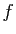 en
en 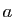 est
verticale, alors
est
verticale, alors 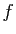 n'est pas dérivable en
n'est pas dérivable en 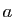 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales