Comme si cela ne suffisait pas, nous avons encore une difficulté à
ajouter ; que se passe-t-il si l'intégrale définissant une
fonction est prise sur un intervalle infini, ou bien si la fonction
à intégrer tend vers l'infini en un point ? La
convergence d'une intégrale s'étudie en isolant les «
problèmes» s'il y en a plusieurs. Chaque type de problème peut
ensuite se ramener par un changement de variable, au cas d'une
intégrale sur
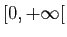 . Afin de ne pas alourdir les notations,
nous nous limiterons à ce dernier cas. Soit
. Afin de ne pas alourdir les notations,
nous nous limiterons à ce dernier cas. Soit
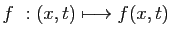 une fonction définie sur
une fonction définie sur
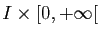 , où
, où  est un intervalle de
est un intervalle de
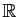 . Supposons que
l'intégrale de l'application partielle
. Supposons que
l'intégrale de l'application partielle
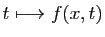 soit
convergente sur
soit
convergente sur
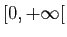 . Nous souhaitons
étudier la fonction qui à
. Nous souhaitons
étudier la fonction qui à 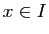 associe
associe
Comme vous le savez, une intégrale convergente est définie comme
une limite d'intégrales sur des intervalles bornés. Posons
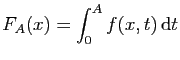
donc
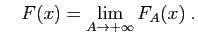
Les résultats de la section précédente donnent des conditions
sous laquelle 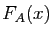 est continue, dérivable, intégrable,
pour
est continue, dérivable, intégrable,
pour 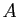 fixé. Pour passer à la limite quand
fixé. Pour passer à la limite quand 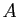 tend vers
l'infini, on ajoute comme d'habitude une hypothèse de convergence
uniforme.
tend vers
l'infini, on ajoute comme d'habitude une hypothèse de convergence
uniforme.
Définition 7
- On dit que l'intégrale
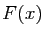 converge simplement si
converge simplement si
- On dit que l'intégrale
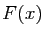 converge uniformément si
converge uniformément si
Sous l'hypothèse de convergence uniforme, les résultats sont bien
ceux que vous attendez.
Théorème 18
Si la fonction  est continue sur
est continue sur
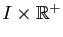 et
si l'intégrale
et
si l'intégrale 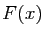 converge
uniformément, alors la fonction
converge
uniformément, alors la fonction 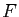 est continue sur
est continue sur  .
.
Théorème 19
On suppose que la dérivée
partielle
existe et est continue sur
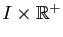 .
On suppose de plus que son intégrale
.
On suppose de plus que son intégrale
converge uniformément.
Alors la fonction 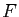 est continûment dérivable sur
est continûment dérivable sur  et :
et :
Nous ne donnerons la démonstration que pour la continuité : les deux
autres résultats ont des démonstrations très proches, que nous
vous engageons vivement à écrire à titre d'exercice.
Démonstration : [du théorème 18]
Soit 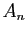 une suite de réels, telle que
une suite de réels, telle que
Pour tout
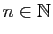 , posons
, posons
Pour tout 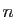 , fixé, la fonction
, fixé, la fonction 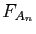 est continue, par application
du théorème 15. Par définition, la suite
de fonctions
est continue, par application
du théorème 15. Par définition, la suite
de fonctions
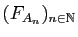 converge (simplement) vers
converge (simplement) vers
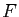 . Il suffit de montrer que la convergence est uniforme pour en
déduire la continuité de
. Il suffit de montrer que la convergence est uniforme pour en
déduire la continuité de 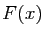 , par le théorème
4. C'est précisément ce qu'affirme l'hypothèse.
, par le théorème
4. C'est précisément ce qu'affirme l'hypothèse. Les critères permettant de s'assurer qu'une intégrale
converge uniformément ressemblent fort à ceux des séries.
Les critères permettant de s'assurer qu'une intégrale
converge uniformément ressemblent fort à ceux des séries.
Définition 8
Pour tout
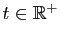 , notons
, notons 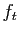 l'application partielle
l'application partielle
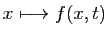 . Rappelons que
. Rappelons que
On dit que l'intégrale 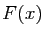 converge normalement,
si l'intégrale
converge normalement,
si l'intégrale
converge
Proposition 3
Si une intégrale converge normalement sur un intervalle, alors elle
converge uniformément sur ce même intervalle.
Démonstration : Par définition de la norme uniforme, pour tout 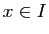 ,
,
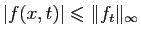 . Par le théorème de comparaison
des intégrales,
. Par le théorème de comparaison
des intégrales,
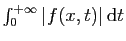 converge,
donc
converge,
donc
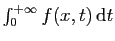 converge
absolument.
converge
absolument.
Le dernier majorant est le reste d'une intégrale
convergente, et il ne dépend pas de  : la convergence est bien
uniforme.
: la convergence est bien
uniforme.  Il n'est pas indispensable de calculer
Il n'est pas indispensable de calculer
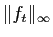 explicitement : il suffit d'en connaître un
majorant fonction de
explicitement : il suffit d'en connaître un
majorant fonction de 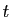 , dont l'intégrale soit convergente.
, dont l'intégrale soit convergente.
L'utilisation de ce corollaire est tellement fréquente, qu'on a
donné un nom à cette situation : on parle de convergence
dominée.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
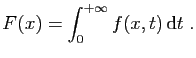
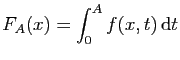 donc
donc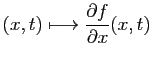
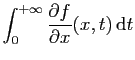
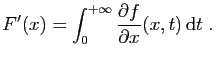
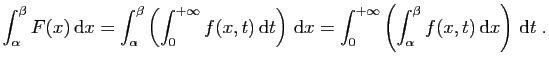
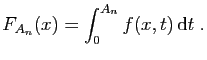
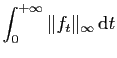
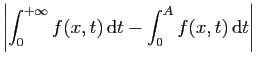
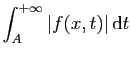
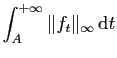
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales