Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours :
Soit
![$ I=]\alpha,\beta[$](img736.gif) un intervalle ouvert de
un intervalle ouvert de
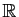 ,
, ![$ J=[a,b]$](img386.gif) un intervalle
fermé borné, et
un intervalle
fermé borné, et 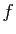 une fonction continue sur
une fonction continue sur 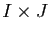 ,
à valeurs dans
,
à valeurs dans
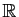 . On considère la fonction
. On considère la fonction 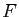 définie pour
tout
définie pour
tout 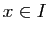 par
par
- Donner la définition de la continuité uniforme, pour une fonction
de
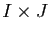 dans
dans
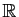 .
.
- Énoncer le théorème de Heine pour une fonction de deux variables.
- Justifier l'existence de
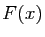 . Démontrer que
. Démontrer que 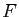 est continue sur
est continue sur 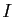 .
.
- On suppose que la dérivée partielle
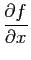 est définie et continue sur
est définie et continue sur
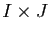 . Montrer que pour tout
. Montrer que pour tout
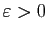 , il existe
, il existe 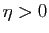 tel que
tel que
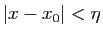 entraîne, pour tout
entraîne, pour tout
![$ t\in
[a,b]$](img382.gif) ,
,
- En déduire que
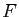 est dérivable en
est dérivable en 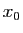 , de dérivée :
, de dérivée :
Exercice 1 :
On considère la suite 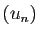 de fonctions définies sur
de fonctions définies sur
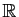 par :
par :
- Justifier la convergence de l'intégrale
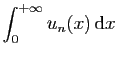 .
.
- Soit
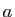 un réel positif ou nul. Vérifier que :
un réel positif ou nul. Vérifier que :
(On pourra intégrer par parties
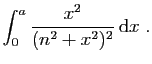 )
)
En déduire
- Montrer que la série
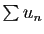 converge normalement sur
converge normalement sur ![$ [0,a]$](img612.gif) .
.
- En déduire que
- Démontrer l'inégalité
En déduire que
- Comparer
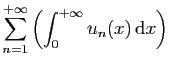
et
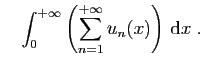
Que pouvez-vous en conclure ?
Exercice 2 :
On considère la fonction zéta de Riemann, définie sur
![$ ]1,+\infty[$](img750.gif) par :
par :
On pose
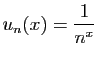 .
.
- Démontrer que la série
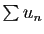 est normalement
convergente sur tout intervalle
est normalement
convergente sur tout intervalle
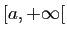 , pour
, pour 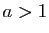 . En
déduire que
. En
déduire que 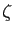 est continue sur
est continue sur
![$ ]1,+\infty[$](img750.gif) .
.
- Pour tout
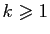 , calculer
, calculer 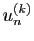 .
Démontrer que la série
.
Démontrer que la série
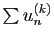 est normalement
convergente sur tout intervalle
est normalement
convergente sur tout intervalle
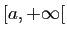 , pour
, pour 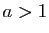 . En
déduire que
. En
déduire que 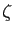 est de classe
est de classe
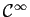 sur
sur
![$ ]1,+\infty[$](img750.gif) .
.
- Montrer que, pour tout
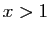 ,
,
- En déduire :
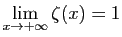
et
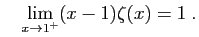
- Pour tout
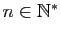 , on pose
, on pose
Montrer que pour tout
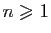 et pour tout
et pour tout 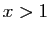 ,
,
- Montrer que la série
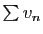 est uniformément convergente sur
tout intervalle
est uniformément convergente sur
tout intervalle
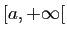 , pour
, pour 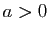 .
.
- Pour tout
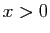 , on pose
, on pose
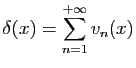 . Montrer que
la fonction
. Montrer que
la fonction 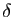 est continue
sur
est continue
sur
![$ ]0,+\infty[$](img516.gif) .
.
- Montrer que :
Cette valeur, approximativement égale à
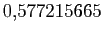 est habituellement notée
est habituellement notée 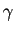 : c'est la
constante d'Euler.
: c'est la
constante d'Euler.
- Déduire de ce qui précède que :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() un intervalle ouvert de
un intervalle ouvert de
![]() ,
, ![]() un intervalle
fermé borné, et
un intervalle
fermé borné, et ![]() une fonction continue sur
une fonction continue sur ![]() ,
à valeurs dans
,
à valeurs dans
![]() . On considère la fonction
. On considère la fonction ![]() définie pour
tout
définie pour
tout ![]() par
par
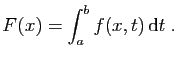
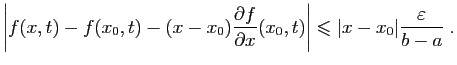
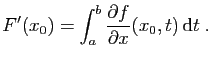
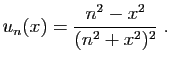
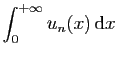 .
.
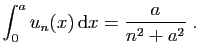
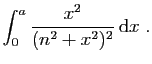 )
)
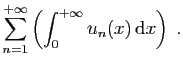
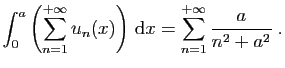
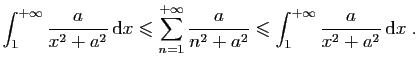
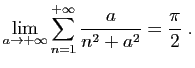
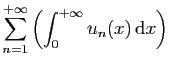 et
et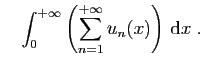
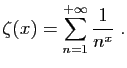
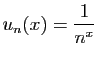 .
.
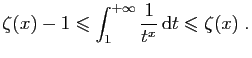
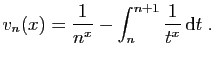
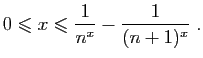
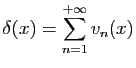 . Montrer que
la fonction
. Montrer que
la fonction 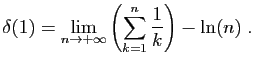
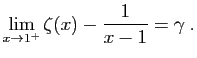
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales