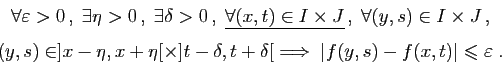
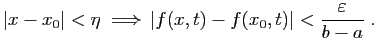
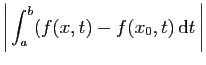 |
|||
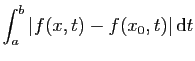 |
|||
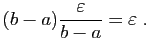 |
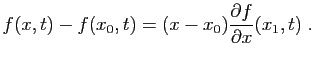
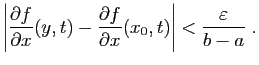
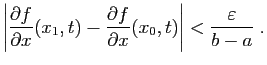
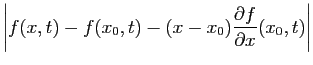 |
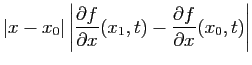 |
||
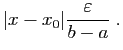 |
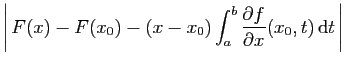 |
|||
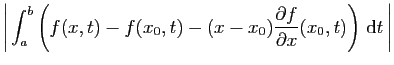 |
|||
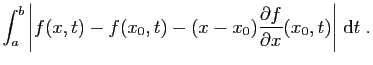 |
La majoration de la question précédente, montre que si
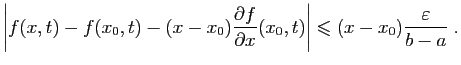
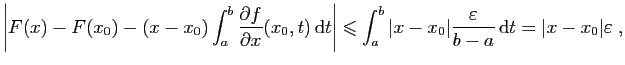
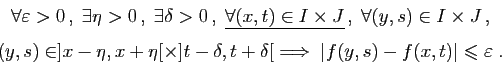
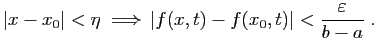
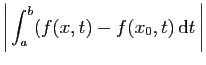 |
|||
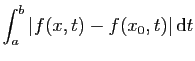 |
|||
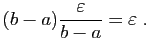 |
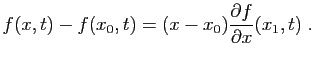
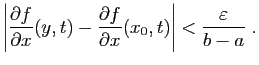
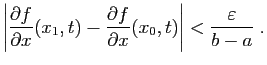
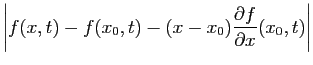 |
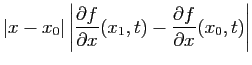 |
||
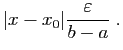 |
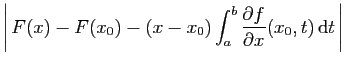 |
|||
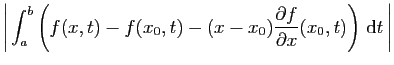 |
|||
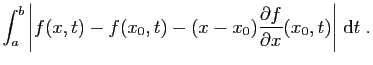 |
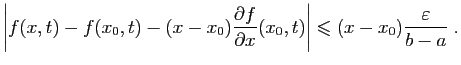
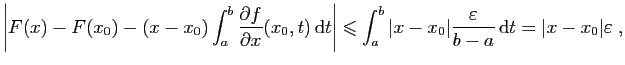
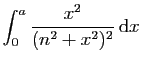 |
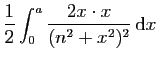 |
||
![$\displaystyle \displaystyle{
\frac{1}{2} \left[-\frac{x}{n^2+x^2}\right]_0^a
+\frac{1}{2}\int_0^a \frac{1}{n^2+x^2} \mathrm{d}x\;.}$](img781.gif) |
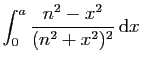 |
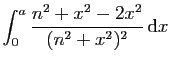 |
||
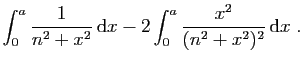 |
![$\displaystyle \int_0^a u_n(x) \mathrm{d}x = \left[-\frac{x}{n^2+x^2}\right]_0^a
=
\frac{a}{n^2+a^2}\;.
$](img785.gif)
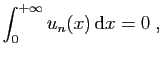
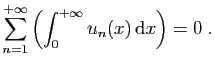
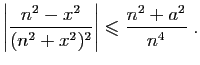
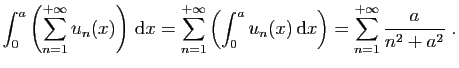
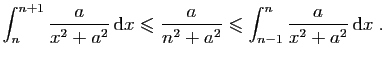
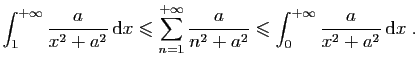
![$\displaystyle \int_{1}^{+\infty} \frac{a}{x^2+a^2} \mathrm{d}x
=
\int_{\frac{1...
...ht]_{\frac{1}{a}}^{+\infty}
= \frac{\pi}{2}-\arctan\left(\frac{1}{a}\right)\;.
$](img798.gif)
![$\displaystyle \int_{0}^{+\infty} \frac{a}{x^2+a^2} \mathrm{d}x
=
\int_0^{+\inf...
...ft[
\arctan\left(\frac{x}{a}\right) \right]_{0}^{+\infty}
= \frac{\pi}{2}\;.
$](img799.gif)
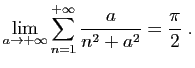
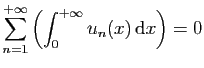 et
et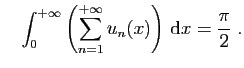
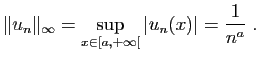
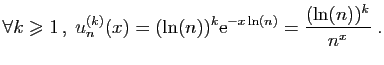
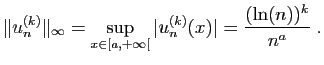
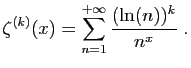
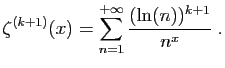
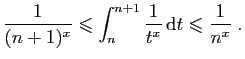
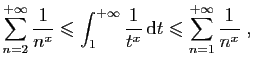
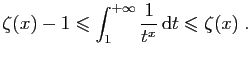
![$\displaystyle \int_1^{+\infty} \frac{1}{t^x} \mathrm{d}t =
\left[\frac{1}{1-x}t^{1-x}\right]_1^{+\infty} =\frac{1}{x-1}\;.
$](img822.gif)
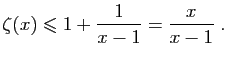
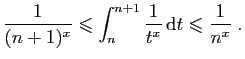
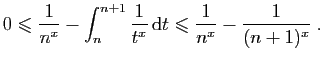
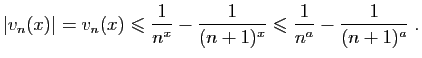
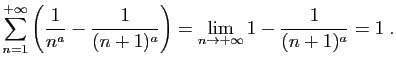
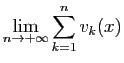 |
|||
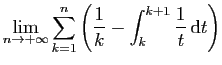 |
|||
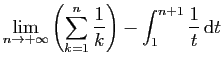 |
|||
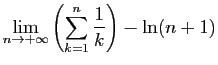 |
|||
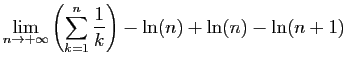 |
|||
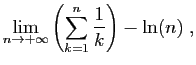 |
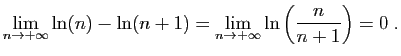
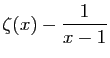 |
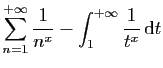 |
||
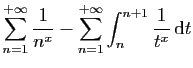 |
|||
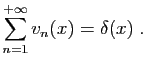 |
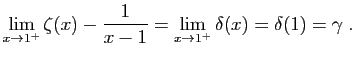
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales