- Démontrer que la suite
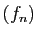 converge simplement vers la
fonction nulle sur
converge simplement vers la
fonction nulle sur ![$ [0,1]$](img149.gif)
- Montrer que
 admet un maximum en
admet un maximum en
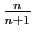 et calculer ce
maximum.
et calculer ce
maximum.
- La suite
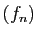 converge-t-elle uniformément sur
converge-t-elle uniformément sur ![$ [0,1]$](img149.gif) ?
?
- Calculer
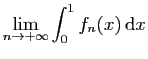 .
.
- Reprendre les questions précédentes pour
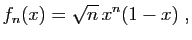 puis
puis 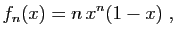 puis
puis 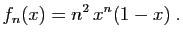
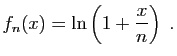
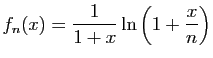 puis
puis 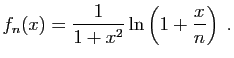
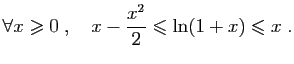
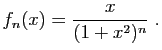
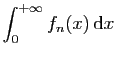
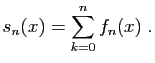
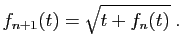
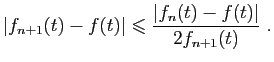
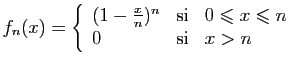
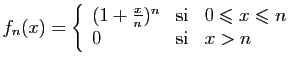
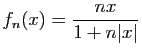
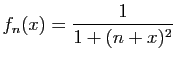
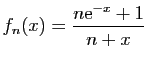
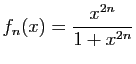
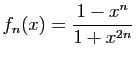
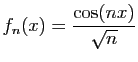
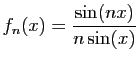
![$ \displaystyle{
f_n(x) = \left\{\begin{array}{lcl}
nx&\mbox{si}& x\in [0,\frac{1}{n}[\\
\frac{n(x-1)}{1-n}&\mbox{si}& x\in [\frac{1}{n},1]
\end{array}\right.
}$](img631.gif)
![$ \displaystyle{
f_n(x) = \left\{\begin{array}{lcl}
\sqrt{n}x&\mbox{si}& x\in [0...
...rac{n(x-1)}{(1-n)\sqrt{n}}&\mbox{si}& x\in [\frac{1}{n},1]
\end{array}\right.
}$](img632.gif)
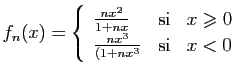
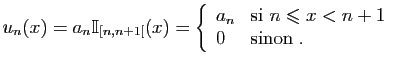
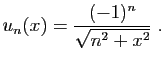
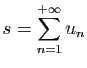
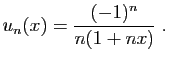
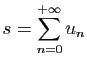
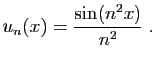
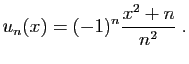
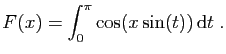
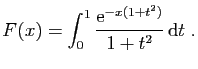
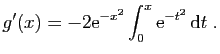
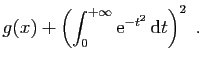
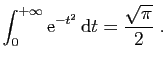
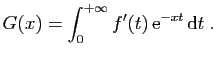
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales