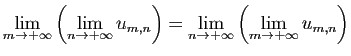
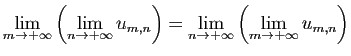
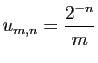
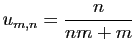
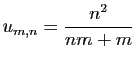
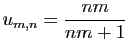
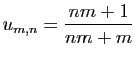
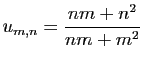
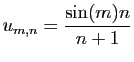
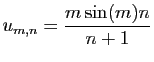
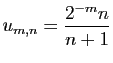
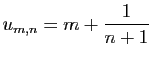
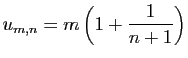
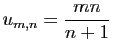
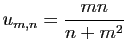
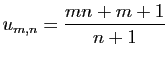
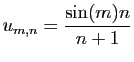
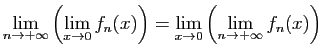
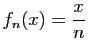
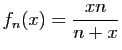
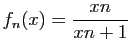
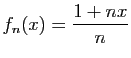
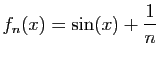
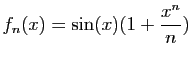
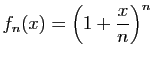
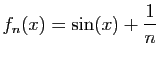
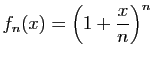
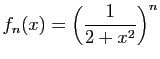
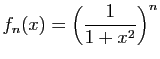
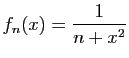
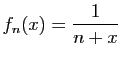
![$\displaystyle \forall x\in]-1,1[\;,\quad \sum_{n=0}^{+\infty}
u_n(x) = s(x)\;.
$](img547.gif)
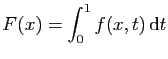 .
Parmi les affirmations suivantes lesquelles sont vraies,
lesquelles sont fausses et pourquoi ?
.
Parmi les affirmations suivantes lesquelles sont vraies,
lesquelles sont fausses et pourquoi ?
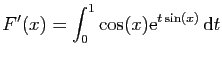 .
.
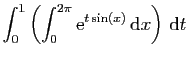 .
.
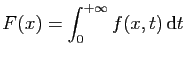 .
Parmi les affirmations suivantes lesquelles sont vraies,
lesquelles sont fausses et pourquoi ?
.
Parmi les affirmations suivantes lesquelles sont vraies,
lesquelles sont fausses et pourquoi ?
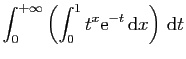 .
.
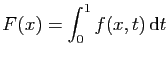 .
Parmi les affirmations suivantes lesquelles sont vraies,
lesquelles sont fausses et pourquoi ?
.
Parmi les affirmations suivantes lesquelles sont vraies,
lesquelles sont fausses et pourquoi ?
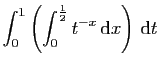 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales