Intuitivement, une courbe dans l'espace de dimension 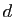 est un objet qui peut être décrit par un point qui évolue au cours du temps. Autrement dit, il suffit d'un paramètre pour le décrire, le temps. On dit d'un tel objet qu'il est
est un objet qui peut être décrit par un point qui évolue au cours du temps. Autrement dit, il suffit d'un paramètre pour le décrire, le temps. On dit d'un tel objet qu'il est 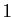 -dimensionnel. Le fait de décrire une courbe par un paramètre qui évolue revient à considérer une application
-dimensionnel. Le fait de décrire une courbe par un paramètre qui évolue revient à considérer une application
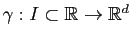 . Quand le paramètre
. Quand le paramètre 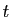 parcourt l'intervalle
parcourt l'intervalle 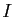 , le point
, le point 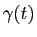 parcourt la courbe. Une telle application
parcourt la courbe. Une telle application 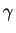 est une courbe paramétrée. On se concentre ici sur l'étude des courbes paramétrées de
est une courbe paramétrée. On se concentre ici sur l'étude des courbes paramétrées de
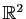 et de
et de
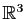 .
.
Définition des courbes paramétrées
L'ensemble
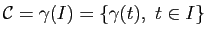 est appelé le support géométrique de
est appelé le support géométrique de
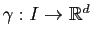 . On dit que
. On dit que
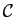 est une courbe géométrique et que
est une courbe géométrique et que 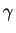 est une paramétrisation de
est une paramétrisation de
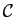 . On peut remarquer que la courbe paramétrée comporte plus d'informations que la courbe géométrique : quand
. On peut remarquer que la courbe paramétrée comporte plus d'informations que la courbe géométrique : quand 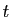 parcourt l'intervalle
parcourt l'intervalle 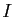 , le point
, le point 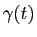 parcourt
parcourt
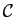 . Autrement dit, la courbe paramétrée donne non seulement le support géométrique, mais aussi une façon de le parcourir.
Dans la suite, quand on considèrera la restriction d'une courbe
. Autrement dit, la courbe paramétrée donne non seulement le support géométrique, mais aussi une façon de le parcourir.
Dans la suite, quand on considèrera la restriction d'une courbe 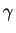 à un intervalle fermé
à un intervalle fermé
![$ [a,b]\subset I$](img52.gif) , on écrira
, on écrira
![$ \gamma:[a,b]\to\mathbb{R}^d$](img53.gif) . Si
. Si 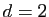 , on dit que la courbe est plane.
, on dit que la courbe est plane.
Figure 1:
Courbe paramétrée
|
|
Exemple :
Le support géométrique de la courbe paramétrée
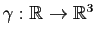 donnée par
donnée par
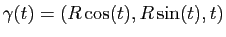 est une hélice (Figure 2).
est une hélice (Figure 2).
Prenons une route allant de Grenoble à Chamrousse et modélisons la par une courbe géométrique
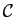 ! Prenons maintenant une voiture qui part de Grenoble à un instant
! Prenons maintenant une voiture qui part de Grenoble à un instant 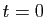 et arrive à Chamrousse à un instant
et arrive à Chamrousse à un instant 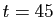 minutes. Le trajet de cette voiture est naturellement modélisé par la courbe paramétrée
minutes. Le trajet de cette voiture est naturellement modélisé par la courbe paramétrée
![$ \gamma : [0,45]\to \mathcal{C}\subset \mathbb{R}^3$](img61.gif) qui à chaque instant
qui à chaque instant 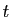 , donne la position
, donne la position 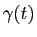 de la voiture. Prenons maintenant un vélo qui va parcourir ce même trajet mais en mettant bien entendu un peu plus de temps, par exemple
de la voiture. Prenons maintenant un vélo qui va parcourir ce même trajet mais en mettant bien entendu un peu plus de temps, par exemple 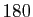 minutes. Cela nous définit une autre paramétrisation
minutes. Cela nous définit une autre paramétrisation
![$ \widetilde{\gamma} : [0,180] \to \mathcal{C}\subset \mathbb{R}^3$](img63.gif) qui est différente de
qui est différente de 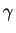 , mais qui a exactement le même support géométrique
, mais qui a exactement le même support géométrique
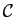 .
.
De même, pour prendre un exemple "plus mathématique", considérons la courbe paramétrée
![$ \gamma : [0,1] \to \mathbb{R}^2$](img64.gif) donnée par
donnée par
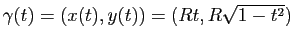 . De l'équation
. De l'équation
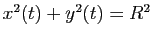 , on déduit que
, on déduit que 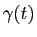 appartient au cercle de rayon
appartient au cercle de rayon 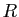 et de centre
et de centre 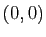 . Plus précisément, le support géométrique de
. Plus précisément, le support géométrique de 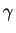 est le quart de cercle entre les points
est le quart de cercle entre les points 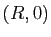 et
et 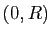 . Or ce support géométrique admet aussi une autre paramétrisation
. Or ce support géométrique admet aussi une autre paramétrisation
![$ \widetilde{\gamma} : [0,{\pi \over 2}]\to \mathbb{R}^2$](img71.gif) donnée par
donnée par
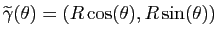 .
Ainsi, une même courbe géométrique peut avoir plusieurs paramétrisations.
.
Ainsi, une même courbe géométrique peut avoir plusieurs paramétrisations.
Reparamétrisation
Il est possible de reparamétrer une courbe. Pour cela, on rappelle la notion de difféomorphisme.
Définition 2
Soient 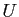 et
et 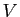 deux domaines ouverts de
deux domaines ouverts de
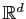 .
.
Une application 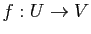 est un
est un 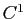 difféomorphisme si :
difféomorphisme si :
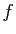 est une bijection de
est une bijection de 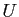 dans
dans 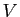 .
.
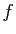 et
et 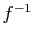 sont toutes les deux de classe
sont toutes les deux de classe 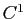 .
.
Prenons maintenant une courbe paramétrée
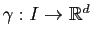 de classe
de classe 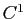 et un difféomorphisme
et un difféomorphisme
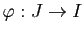 (avec
(avec 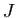 un intervalle ouvert de
un intervalle ouvert de
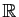 ). Alors
). Alors
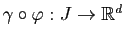 est une courbe paramétrée qui a exactement le même support géométrique que
est une courbe paramétrée qui a exactement le même support géométrique que 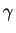 . On dit alors que
. On dit alors que 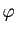 est un changement de variable admissible et que
est un changement de variable admissible et que
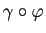 est une reparamétrisation de
est une reparamétrisation de 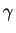 .
.
Courbes régulières, espace tangent
Intuitivement, la tangente en un point
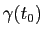 à une courbe paramétrée
à une courbe paramétrée
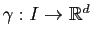 est la limite des droites passant par
est la limite des droites passant par 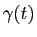 et
et
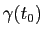 quand
quand 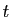 tend vers
tend vers 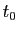 . Cela peut se formaliser de la manière suivante :
. Cela peut se formaliser de la manière suivante :
La proposition suivante indique qu'une dérivée non nulle de la paramétrisation donne un vecteur tangent.
Proposition 1
Soit
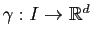 une courbe paramétrée de classe
une courbe paramétrée de classe 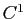 . Si
. Si
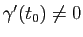 , alors
, alors
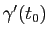 est un vecteur tangent à la courbe
est un vecteur tangent à la courbe 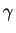 en
en
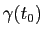 .
.
Démonstration : Comme 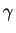 est de classe
est de classe 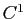 , on a :
, on a :
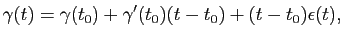
avec
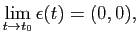
ce qui permet de conclure.
Figure 3:
Tangente à une courbe paramétrée
|
|
Définition 4
Une courbe paramétrée
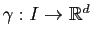 de classe
de classe 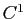 est dite régulière si pour tout
est dite régulière si pour tout 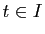
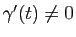 .
.
Remarques :
Longueur d'une courbe
Comment mesurer la longueur d'une courbe ? Une façon naturelle de procéder consiste à approcher cette longueur par la longueur d'une ligne polygonale dont les sommets sont sur la courbe. La longueur de la ligne polygonale est clairement inférieure à celle de la courbe, mais on imagine bien que si on rajoute des sommets en diminuant la distance entre deux sommets consécutifs, la longueur de la ligne polygonale va tendre vers la longueur de la courbe. La définition de la longueur d'une courbe repose sur cette idée (Figure 4):
Remarque :
La longueur ne dépend pas de la paramétrisation.
Figure 4:
Longueur d'une courbe paramétrée
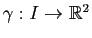 . Si on augmente la densité des sommets de la ligne polygonale
. Si on augmente la densité des sommets de la ligne polygonale 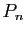 le long de la courbe, alors la longueur de
le long de la courbe, alors la longueur de 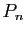 approche celle de la courbe.
approche celle de la courbe.
|
|
La définition précédente est géométrique et correspond à l'intuition que l'on peut avoir de la longueur. Ceci dit, elle n'est pas forcément pratique pour effectuer des calculs. Le théorème suivant exprime la longueur d'une courbe paramétrée par une formule intégrale.
Théorème 1
Soit
![$ \gamma : [a,b] \to \mathbb{R}^3$](img113.gif) une courbe paramétrée de classe
une courbe paramétrée de classe 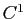 . Alors
. Alors 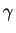 est rectifiable et on a :
est rectifiable et on a :
Démonstration : Considérons une subdivision
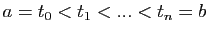 de l'intervalle
de l'intervalle ![$ [a,b]$](img108.gif) . Nous avons pour tout
. Nous avons pour tout
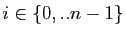 :
:
Cela implique en sommant sur 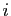 :
:
En passant maintenant au supremum sur toutes les subdivisions, on obtient que 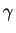 est rectifiable et vérifie :
est rectifiable et vérifie :
Montrons maintenant l'égalité souhaitée. Pour cela, introduisons la fonction
![$ \phi:[a,b]\to \mathbb{R}$](img120.gif) qui donne la longueur de la courbe entre les paramètres
qui donne la longueur de la courbe entre les paramètres 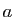 et
et 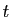 :
:
Prenons
![$ t \in [a,b]$](img123.gif) et
et 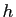 vérifiant
vérifiant
![$ t+h \in [a,b]$](img125.gif) . La longueur de la courbe entre les paramètres
. La longueur de la courbe entre les paramètres 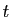 et
et 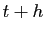 étant plus longue que la longueur du segment reliant
étant plus longue que la longueur du segment reliant 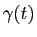 à
à
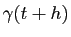 , on a :
, on a :
On en déduit l'encadrement suivant :
Les membres de droite et de gauche ont la même limite
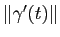 , ce qui implique que
, ce qui implique que 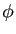 est dérivable en
est dérivable en 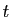 et que l'on a
et que l'on a
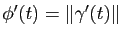 .
.
Exemple :La longueur de l'hélice paramétrée par
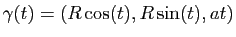 avec
avec
![$ \gamma: [0,2\pi] \to \mathbb{R}^3$](img134.gif) est donnée par :
est donnée par :
Remarquons au passage que si 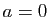 , on retrouve que la longueur d'un cercle de rayon
, on retrouve que la longueur d'un cercle de rayon 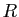 vaut
vaut 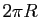 .
.
Paramétrisation par abscisse curviligne
Maintenant que l'on sait calculer la longueur d'une courbe, il est possible de paramétrer une courbe par sa longueur. Pour expliquer ce que représente cette paramétrisation, on peut reprendre l'exemple de la courbe
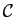 qui modélise la route Grenoble-Chamrousse. On a déjà donné deux paramétrisations possibles de cette courbe, mais il est aussi possible d'en définir une troisième en repérant chaque point de
qui modélise la route Grenoble-Chamrousse. On a déjà donné deux paramétrisations possibles de cette courbe, mais il est aussi possible d'en définir une troisième en repérant chaque point de
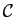 par sa distance au point d'origine, à savoir Grenoble. La longueur du trajet étant de
par sa distance au point d'origine, à savoir Grenoble. La longueur du trajet étant de 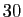 kilomètres, cela nous définit naturellement la courbe paramétrée
kilomètres, cela nous définit naturellement la courbe paramétrée
![$ \gamma : [0,30]\to \mathbb{R}^3$](img139.gif) qui à chaque longueur
qui à chaque longueur
![$ s\in[0,30]$](img140.gif) associe le point
associe le point 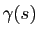 sur la courbe
sur la courbe
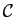 qui est à une distance
qui est à une distance 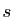 du point de départ. Cette paramétrisation est dite normale ou par abscisse curviligne. Elle est assez naturelle dans le sens ou elle ne dépend pas de la vitesse d'un véhicule qui parcourt cette courbe (plus exactement, cette vitesse est constante). Formellement, on définit :
du point de départ. Cette paramétrisation est dite normale ou par abscisse curviligne. Elle est assez naturelle dans le sens ou elle ne dépend pas de la vitesse d'un véhicule qui parcourt cette courbe (plus exactement, cette vitesse est constante). Formellement, on définit :
En pratique, on n'a pas forcément une paramétrisation normale. Si on veut en avoir une, il faut reparamétrer. Pour cela, on a besoin de la notion d'abscisse curviligne.
Géométriquement,
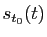 est la longueur de la courbe géométrique
est la longueur de la courbe géométrique
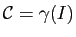 entre les points
entre les points
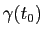 et
et 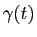 . Le résultat suivant nous indique que toute courbe paramétrée régulière de classe
. Le résultat suivant nous indique que toute courbe paramétrée régulière de classe 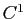 peut être reparamétrée par abscisse curviligne.
peut être reparamétrée par abscisse curviligne.
Démonstration : Admise.
Intuitivement, si on "déroule" une courbe géométrique
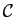 de longueur
de longueur 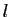 le long d'une droite, on obtient un segment qui est aussi de longueur
le long d'une droite, on obtient un segment qui est aussi de longueur 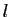 et qui peut être identifié à l'intervalle
et qui peut être identifié à l'intervalle ![$ I=[0,l]$](img158.gif) . La correspondance point par point entre
. La correspondance point par point entre 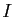 et
et
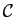 donne naturellement une paramétrisation normale
donne naturellement une paramétrisation normale
![$ \widetilde{\gamma} : [0,l] \to\mathcal{C}$](img159.gif) .
Par convention, on note souvent
.
Par convention, on note souvent 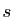 le paramètre d'une courbe paramétrée par abscisse curviligne et on note souvent
le paramètre d'une courbe paramétrée par abscisse curviligne et on note souvent 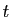 le paramètre dans le cas d'une paramétrisation quelconque.
le paramètre dans le cas d'une paramétrisation quelconque.
Proposition 2
Soit
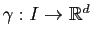 une courbe paramétrée de classe
une courbe paramétrée de classe 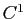 . Alors on a :
. Alors on a :
la paramétrisation
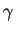
est normale
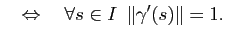
Démonstration : Si la paramétrisation est normale, alors l'abscisse curviligne à partir du point 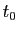 de
de 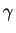 vérifie pour tout
vérifie pour tout 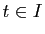 :
:
En dérivant, cela donne pour tout 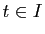 :
:
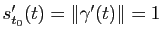 .
.
Réciproquement, si pour tout 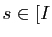 on a
on a
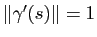 , alors pour tout
, alors pour tout
![$ [t_1,t_2] \subset I$](img143.gif) :
:

Exemple :On considère la courbe paramétrée
![$ \gamma:]0,1[\to\mathbb{R}^2$](img167.gif) définie par
définie par
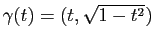 . L'abscisse curviligne
. L'abscisse curviligne
![$ s_{0}:]0,1[\to \mathbb{R}$](img169.gif) est donnée par :
est donnée par :
La fonction
![$ \arcsin:[0,1[\to]0,\pi/2[$](img171.gif) est une bijection. La reparamétrisation
est une bijection. La reparamétrisation
![$ \widetilde{\gamma}=\gamma \circ s_0^{-1}:]0,\pi/2[\to\mathbb{R}^2$](img172.gif) est donnée par :
est donnée par :
On remarque que cela correspond à une paramétrisation du quart de cercle de rayon 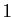 entre les points de coordonnées
entre les points de coordonnées 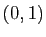 et
et 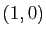 . Le paramètre
. Le paramètre 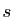 correspond à l'angle entre
correspond à l'angle entre
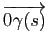 et le vecteur de coordonnées
et le vecteur de coordonnées 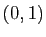 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() donnée par
donnée par
![]() est une hélice (Figure 2).
est une hélice (Figure 2).
![]() ! Prenons maintenant une voiture qui part de Grenoble à un instant
! Prenons maintenant une voiture qui part de Grenoble à un instant ![]() et arrive à Chamrousse à un instant
et arrive à Chamrousse à un instant ![]() minutes. Le trajet de cette voiture est naturellement modélisé par la courbe paramétrée
minutes. Le trajet de cette voiture est naturellement modélisé par la courbe paramétrée
![]() qui à chaque instant
qui à chaque instant ![]() , donne la position
, donne la position ![]() de la voiture. Prenons maintenant un vélo qui va parcourir ce même trajet mais en mettant bien entendu un peu plus de temps, par exemple
de la voiture. Prenons maintenant un vélo qui va parcourir ce même trajet mais en mettant bien entendu un peu plus de temps, par exemple ![]() minutes. Cela nous définit une autre paramétrisation
minutes. Cela nous définit une autre paramétrisation
![]() qui est différente de
qui est différente de ![]() , mais qui a exactement le même support géométrique
, mais qui a exactement le même support géométrique
![]() .
.
![]() donnée par
donnée par
![]() . De l'équation
. De l'équation
![]() , on déduit que
, on déduit que ![]() appartient au cercle de rayon
appartient au cercle de rayon ![]() et de centre
et de centre ![]() . Plus précisément, le support géométrique de
. Plus précisément, le support géométrique de ![]() est le quart de cercle entre les points
est le quart de cercle entre les points ![]() et
et ![]() . Or ce support géométrique admet aussi une autre paramétrisation
. Or ce support géométrique admet aussi une autre paramétrisation
![]() donnée par
donnée par
![]() .
Ainsi, une même courbe géométrique peut avoir plusieurs paramétrisations.
.
Ainsi, une même courbe géométrique peut avoir plusieurs paramétrisations.
![]() à une courbe paramétrée
à une courbe paramétrée
![]() est la limite des droites passant par
est la limite des droites passant par ![]() et
et
![]() quand
quand ![]() tend vers
tend vers ![]() . Cela peut se formaliser de la manière suivante :
. Cela peut se formaliser de la manière suivante :
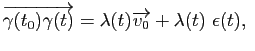 avec
avec 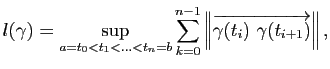
![\includegraphics[height=5cm]{longueur2}](img111.gif)
![\includegraphics[height=5cm]{longueur4}](img112.gif)
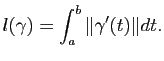
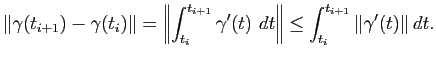
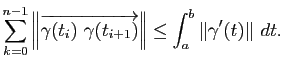
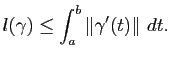
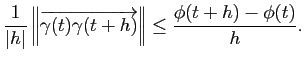
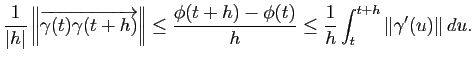
![]() avec
avec
![]() est donnée par :
est donnée par :
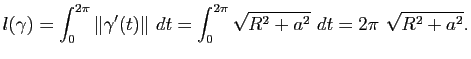
![]() qui modélise la route Grenoble-Chamrousse. On a déjà donné deux paramétrisations possibles de cette courbe, mais il est aussi possible d'en définir une troisième en repérant chaque point de
qui modélise la route Grenoble-Chamrousse. On a déjà donné deux paramétrisations possibles de cette courbe, mais il est aussi possible d'en définir une troisième en repérant chaque point de
![]() par sa distance au point d'origine, à savoir Grenoble. La longueur du trajet étant de
par sa distance au point d'origine, à savoir Grenoble. La longueur du trajet étant de ![]() kilomètres, cela nous définit naturellement la courbe paramétrée
kilomètres, cela nous définit naturellement la courbe paramétrée
![]() qui à chaque longueur
qui à chaque longueur
![]() associe le point
associe le point ![]() sur la courbe
sur la courbe
![]() qui est à une distance
qui est à une distance ![]() du point de départ. Cette paramétrisation est dite normale ou par abscisse curviligne. Elle est assez naturelle dans le sens ou elle ne dépend pas de la vitesse d'un véhicule qui parcourt cette courbe (plus exactement, cette vitesse est constante). Formellement, on définit :
du point de départ. Cette paramétrisation est dite normale ou par abscisse curviligne. Elle est assez naturelle dans le sens ou elle ne dépend pas de la vitesse d'un véhicule qui parcourt cette courbe (plus exactement, cette vitesse est constante). Formellement, on définit :
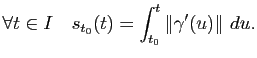
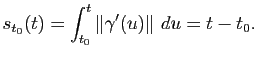
![$\displaystyle l(\gamma_{\vert[t_1,t_2]}) = \int_{t_1}^{t_2} \Vert\gamma'(s)\Vert ds = t_2 -t_1.
$](img166.gif)
![]() définie par
définie par
![]() . L'abscisse curviligne
. L'abscisse curviligne
![]() est donnée par :
est donnée par :
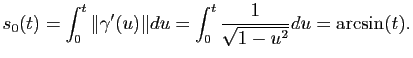
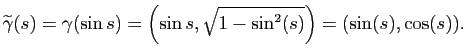
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales