Devoir

Essayez de bien rédiger vos réponses, sans vous reporter ni au cours, ni au corrigé. Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez vos réponses avec le corrigé.

Question de cours : Soit 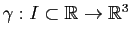$\gamma:I\subset \mathbb{R}\to\mathbb{R}^3$ une courbe paramétrée de classe 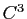$C^3$, dont tous les points sont biréguliés.

• Donner la définition du repère de Serret-Frenet.
• Donner les formules de Serret-Frenet.

Exercice 1   Montrer que les courbes planes régulières de classe 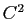$C^2$ à courbure constante sont des arcs de cercle.
(On pourra considérer les paramétrisations par abscisse curviligne et montrer que le centre de courbure est constant.)

Exercice 2   Soient $R$ et $a$ deux nombres réels. On considère la courbe paramétrée suivante :

$$\begin{array}{rrll} \gamma :& \mathbb{R}&\to & \mathbb{R}^3\\ & t &\mapsto & \left( R\cos t,R\sin t, at \right)\\ \end{array}$$

1. Que représente géométriquement cette courbe ?
2. Déterminer une paramétrisation par abscisse curviligne.
3. Calculer le repère de Serret-Frenet.
4. Calculer la courbure $\kappa_a$ de $\gamma$ en tout point. Que remarquez-vous ?
5. Calculer la torsion $\tau_a$ de $\gamma$ en tout point ? Que remarquez-vous ?
6. Calculer les limites
   $$\lim_{a\to 0} \kappa_a$$   et$$\quad \lim_{a\to 0} \tau_a$$
   Pouvait-on s'attendre à ce résultat ?

Exercice 3   On prend deux nombres réels $0<r<R$. On considère le tore de révolution $f:[0,2\pi[\times [0,2\pi[\to\mathbb{R}^3$ paramétré par

$$f(u,v) = \left( \begin{array}{c} (R+r\cos u)\cos v\\ (R+r\cos u)\sin v\\ r\sin u \end{array}\right).$$

1. Représenter cette surface en $3D$. Pourquoi, à votre avis, cette surface est-elle dite "de révolution" ?
2. Calculer l'aire de cette surface.
3. Que représentent géométriquement les courbes $\mathcal{C}_1 = \{f(0,v), v\in [0,2\pi[\}$ et $\mathcal{C}_2 = \{f(u,0), u\in [0,2\pi[\}$ ?
4. Montrer que les vecteurs tangents à ces courbes au point d'intersection $m=f(0,0)$ sont orthogonaux.
5. Calculer en tout point $m$ de la surface la deuxième forme fondamentale $II_m$, ainsi que les courbures et directions principales.
6. En tout point $m=f(u,v)$ de la surface, calculer le produit $G_m$ des deux courbures principales.
   • Déterminer les points $m$ pour lesquels $G_m >0$
   • Déterminer les points $m$ pour lesquels $G_m <0$
   • Déterminer les points $m$ pour lesquels $G_m =0$
7. Interpréter géométriquement ces résultats.