La première technique de calcul consiste à utiliser la
linéarité pour séparer l'intégrale d'une somme en une somme
d'intégrales. L'exemple le plus simple est celui des polynômes.
On peut aussi intégrer
des polynômes en 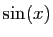 et
et 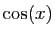 , ou
bien
, ou
bien 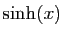 et
et 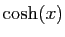 . On utilise pour cela les
formules d'Euler, et les propriétés de l'exponentielle (réelle
ou complexe).
Le principe est le suivant : tout polynôme en
. On utilise pour cela les
formules d'Euler, et les propriétés de l'exponentielle (réelle
ou complexe).
Le principe est le suivant : tout polynôme en 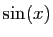 et
et 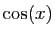 est une combinaison linéaire de termes de la forme
est une combinaison linéaire de termes de la forme
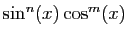 , qu'il s'agit de linéariser,
en les exprimant eux-mêmes
comme combinaisons linéaires de termes en
, qu'il s'agit de linéariser,
en les exprimant eux-mêmes
comme combinaisons linéaires de termes en 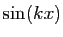 et
et 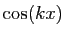 ,
dont on connaît une primitive. Voici un exemple.
,
dont on connaît une primitive. Voici un exemple.
D'où une primitive de
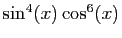 :
:
Observons que les questions de parité permettent de prévoir a
priori que la linéarisation ne contiendra que des 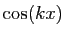 . En
effet,
. En
effet,
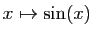 est une fonction impaire et
est une fonction impaire et
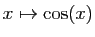 une fonction
paire. Donc si on remplace
une fonction
paire. Donc si on remplace 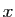 par
par 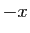 ,
,
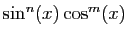 sera
inchangé si
sera
inchangé si 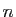 est pair, changé en son opposé si
est pair, changé en son opposé si 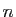 est
impair. Dans le premier cas, la linéarisation ne contiendra que des
cosinus, dans le second cas, elle ne contiendra que des sinus.
La même technique s'utilise aussi pour les cosinus et sinus
hyperboliques.
est
impair. Dans le premier cas, la linéarisation ne contiendra que des
cosinus, dans le second cas, elle ne contiendra que des sinus.
La même technique s'utilise aussi pour les cosinus et sinus
hyperboliques.
Comme autre application de l'exponentielle complexe, signalons la
possibilité d'intégrer des expressions du type
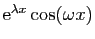 ou
ou
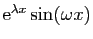 , en les
exprimant comme parties réelles ou imaginaires d'exponentielles
complexes, que l'on peut intégrer formellement comme des
exponentielles réelles. Voici un exemple.
, en les
exprimant comme parties réelles ou imaginaires d'exponentielles
complexes, que l'on peut intégrer formellement comme des
exponentielles réelles. Voici un exemple.
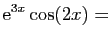
Re
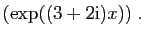
Or une primitive (formelle) de
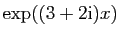 est :
est :
La partie réelle de cette expression est :
qui est donc une primitive de
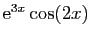 .
.
La seconde technique de calcul à connaître est l'intégration
par parties :
Il faut penser à une intégration par parties quand l'un des
facteurs de la fonction à intégrer a une dérivée plus simple,
essentiellement un polynôme (dériver diminue le degré), 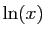 (dérivée
(dérivée 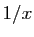 ),
),
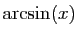 (dérivée
(dérivée
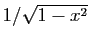 ) ou
) ou
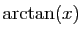 (dérivée
(dérivée 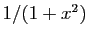 ). Encore faut-il connaître une
primitive de l'autre facteur. Par exemple, pour
). Encore faut-il connaître une
primitive de l'autre facteur. Par exemple, pour
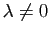 :
:
La technique de calcul d'intégrales (ou de primitives)
la plus importante est le changement de variable.
Il est fortement déconseillé de retenir la formule par
c ur.
Un changement de variable doit se penser de la manière
suivante.
ur.
Un changement de variable doit se penser de la manière
suivante.
- Je souhaite remplacer
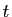 par
par 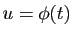 .
.
- J'exprime
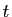 en fonction de
en fonction de 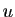 :
:
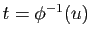 (je m'assure
que
(je m'assure
que 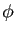 est bien une bijection).
est bien une bijection).
- J'exprime
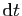 en fonction de
en fonction de 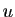 et
et
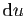 en dérivant
l'expression de
en dérivant
l'expression de 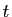 fonction de
fonction de 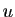 :
:
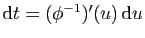 .
.
- J'ajuste les bornes de l'intervalle d'intégration : si
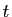 varie de
varie de 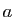 à
à 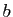 , alors
, alors 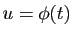 varie de
varie de 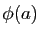 à
à
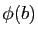 . (Cet ajustement des bornes est la raison pour laquelle il
est conseillé de calculer une primitive comme une intégrale de
. (Cet ajustement des bornes est la raison pour laquelle il
est conseillé de calculer une primitive comme une intégrale de 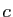 à
à 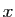 ).
).
- Je remplace
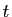 et
et
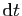 par leurs valeurs en fonction de
par leurs valeurs en fonction de
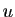 et
et
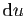 .
.
Comme exemple, nous allons traiter trois primitives d'un type
fréquent, comportant la racine carrée d'un trinôme.
Voici la première.
Notons que la fonction à intégrer est définie sur
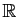 tout entier.
La première étape consiste à mettre le trinôme sous forme
canonique, de manière à faire apparaître l'une des trois expressions
tout entier.
La première étape consiste à mettre le trinôme sous forme
canonique, de manière à faire apparaître l'une des trois expressions
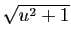 ,
,
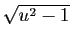 ou
ou
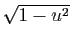 . Nous sommes ici
dans le premier cas.
. Nous sommes ici
dans le premier cas.
Nous devons donc poser :
On obtient :
Voici une situation proche, mais qui du fait des signes
rencontrés dans le trinôme, conduit à des résultats différents.
La fonction à intégrer est définie sur
![$ ]-\infty,-1[\cup]3,+\infty[$](img154.gif) . Nous devons donc supposer que
l'intervalle
. Nous devons donc supposer que
l'intervalle ![$ [c,x]$](img47.gif) est soit inclus dans
est soit inclus dans
![$ ]-\infty,-1[$](img155.gif) , soit dans
, soit dans
![$ ]3,+\infty[$](img156.gif) .
La mise du trinôme sous forme canonique donne :
.
La mise du trinôme sous forme canonique donne :
Nous devons donc poser :
On obtient :
Comme prévu, les primitives ne sont définies que pour
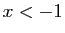 ou
ou 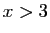 . Remarquez que le signe de
. Remarquez que le signe de
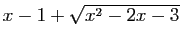 dépend de l'intervalle sur lequel on se
trouve : il est négatif sur
dépend de l'intervalle sur lequel on se
trouve : il est négatif sur
![$ ]-\infty,-1[$](img155.gif) , positif sur
, positif sur
![$ ]3,+\infty[$](img156.gif) .
Voici le dernier cas que l'on peut rencontrer selon le signe du trinôme.
.
Voici le dernier cas que l'on peut rencontrer selon le signe du trinôme.
La fonction à intégrer n'est définie que sur l'intervalle
![$ ]\!-\!1,3[$](img171.gif) . Nous devons donc supposer que l'intervalle
. Nous devons donc supposer que l'intervalle ![$ [c,x]$](img47.gif) est
inclus dans
est
inclus dans ![$ ]-1,3[$](img172.gif) .
La mise du trinôme sous forme canonique donne :
.
La mise du trinôme sous forme canonique donne :
Nous devons donc poser :
On obtient :
Comme prévu, les primitives ne seront définies que pour
![$ x\in ]\!-\!1,3[$](img179.gif) .
Nous verrons plus loin d'autres applications classiques des changements
de variable. Il n'est pas toujours facile de deviner le bon changement
de variable. Pour cela, il faut se laisser guider
par l'expression de
.
Nous verrons plus loin d'autres applications classiques des changements
de variable. Il n'est pas toujours facile de deviner le bon changement
de variable. Pour cela, il faut se laisser guider
par l'expression de 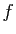 : si elle contient une
fonction
: si elle contient une
fonction 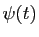 et sa dérivée
et sa dérivée 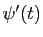 , il pourra être
judicieux de poser
, il pourra être
judicieux de poser 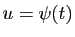 . Dans le cas le plus favorable, la
fonction se met sous la forme
. Dans le cas le plus favorable, la
fonction se met sous la forme
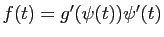 ,
qui est la dérivée de
,
qui est la dérivée de
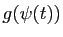 . Il suffira donc de connaître une primitive de
. Il suffira donc de connaître une primitive de 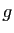 . Ceci ne relève pas directement du
théorème 4, et s'applique d'ailleurs même si
. Ceci ne relève pas directement du
théorème 4, et s'applique d'ailleurs même si
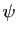 n'est pas monotone. Voici
un exemple, avec
n'est pas monotone. Voici
un exemple, avec
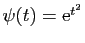 , et
, et
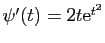 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
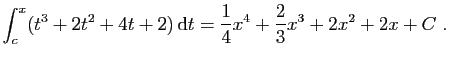
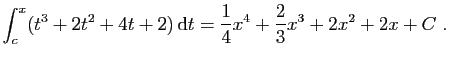
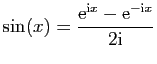
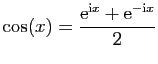
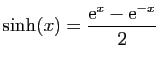
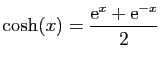
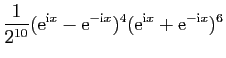
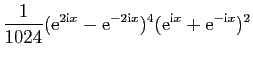
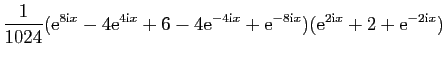
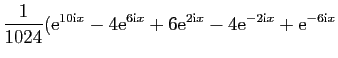
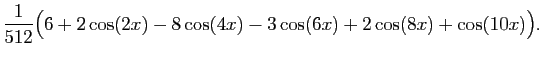
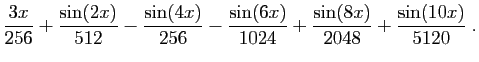
![]() ou
ou
![]() , en les
exprimant comme parties réelles ou imaginaires d'exponentielles
complexes, que l'on peut intégrer formellement comme des
exponentielles réelles. Voici un exemple.
, en les
exprimant comme parties réelles ou imaginaires d'exponentielles
complexes, que l'on peut intégrer formellement comme des
exponentielles réelles. Voici un exemple.
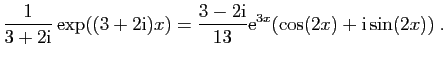
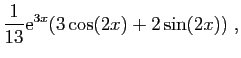
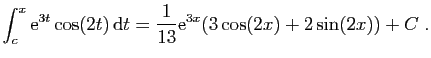
![$\displaystyle \int_{a}^{b} u(x) v'(x) dx = \Big[u(x) v(x)\Big]_{a}^{b}
- \int_{a}^{b} u'(x) v(x) dx\;.
$](img115.gif)
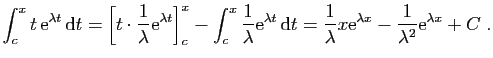
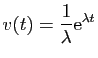
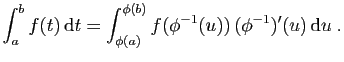
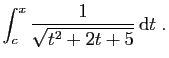
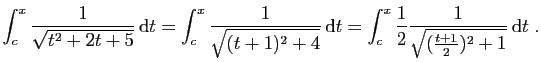
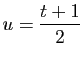 soit
soit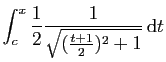
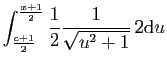
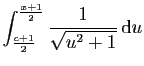
![$\displaystyle \Big[\ln(u+\sqrt{u^2+1})\Big]_{\frac{c+1}{2}}^{\frac{x+1}{2}}$](img149.gif)
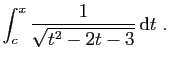
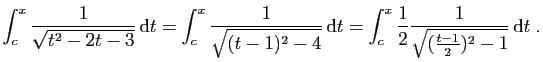
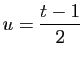 soit
soit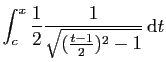
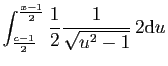
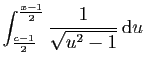
![$\displaystyle \Big[\ln\vert u+\sqrt{u^2-1}\vert\Big]_{\frac{c-1}{2}}^{\frac{x-1}{2}}$](img163.gif)
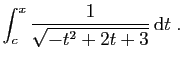
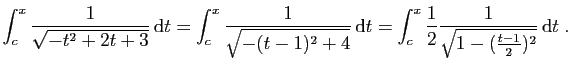
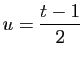 soit
soit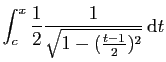
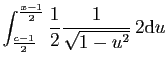
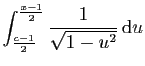
![$\displaystyle \Big[\arcsin(u)\Big]_{\frac{c-1}{2}}^{\frac{x-1}{2}}$](img177.gif)
![$\displaystyle \int_c^x \frac{2t}{1+\mathrm{e}^{-t^2}} \mathrm{d}t =
\int_c^x \...
...thrm{d}t=
\Big[\ln(1+\mathrm{e}^{t^2})\Big]_c^x=
\ln(1+\mathrm{e}^{x^2})+C\;.
$](img189.gif)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales