Rappelons tout d'abord la définition.
Définition 1
On appelle primitive d'une fonction 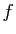 , définie sur un intervalle
, définie sur un intervalle
![$ ]a,b[$](img28.gif) , toute fonction dérivable sur
, toute fonction dérivable sur ![$ ]a,b[$](img28.gif) , dont la dérivée
coïncide avec
, dont la dérivée
coïncide avec 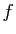 sur
sur ![$ ]a,b[$](img28.gif) .
.
Etant données deux primitives de 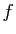 , leur différence doit avoir
une dérivée nulle, et donc être constante. Deux primitives de la
même fonction diffèrent donc par une constante.
Pour spécifier
une primitive particulière, il suffit de fixer sa valeur en un
point. En général, on considère la primitive qui s'annule en un
certain point. Elle s'écrit comme une intégrale, grâce au
théorème suivant, que nous admettrons.
, leur différence doit avoir
une dérivée nulle, et donc être constante. Deux primitives de la
même fonction diffèrent donc par une constante.
Pour spécifier
une primitive particulière, il suffit de fixer sa valeur en un
point. En général, on considère la primitive qui s'annule en un
certain point. Elle s'écrit comme une intégrale, grâce au
théorème suivant, que nous admettrons.
Observons l'écriture
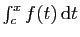 , dans laquelle les deux
lettres
, dans laquelle les deux
lettres 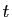 et
et 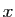 jouent des rôles totalement différents. La
lettre
jouent des rôles totalement différents. La
lettre 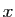 désigne une borne de l'intervalle d'intégration.
Si on la remplace par un réel, par exemple
désigne une borne de l'intervalle d'intégration.
Si on la remplace par un réel, par exemple 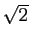 ,
on obtiendra un résultat réel : la valeur de la
fonction
,
on obtiendra un résultat réel : la valeur de la
fonction 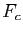 au point
au point 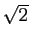 . La variable d'intégration
. La variable d'intégration
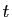 est muette. On ne peut pas la remplacer par un réel. Par contre,
n'importe quelle autre lettre (sauf
est muette. On ne peut pas la remplacer par un réel. Par contre,
n'importe quelle autre lettre (sauf 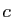 et
et 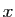 )
pourrait jouer le même rôle. Dans l'écriture des primitives, on
évitera toujours de noter avec la même lettre la variable
d'intégration et une des bornes de l'intervalle.
Observons que n'importe quelle primitive peut être utilisée pour
calculer une intégrale :
)
pourrait jouer le même rôle. Dans l'écriture des primitives, on
évitera toujours de noter avec la même lettre la variable
d'intégration et une des bornes de l'intervalle.
Observons que n'importe quelle primitive peut être utilisée pour
calculer une intégrale :
par la relation de Chasles. L'intégrale de 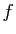 est donc un
accroissement de primitive, qui ne dépend pas de la primitive
choisie. On note :
est donc un
accroissement de primitive, qui ne dépend pas de la primitive
choisie. On note :
Il est commode, en particulier pour les changements de variable, de
conserver des bornes d'intégration, même quand on ne calcule que
des primitives. C'est pourquoi nous continuerons de noter
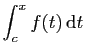 la primitive de
la primitive de 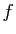 qui s'annule en
qui s'annule en
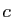 , même s'il est superflu de fixer
, même s'il est superflu de fixer 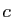 . De notre point de vue, il
n'y a donc aucune différence entre les calculs de primitives et les
calculs d'intégrales. Il est courant d'exprimer les primitives des
fonctions usuelles «à une constante près». Par exemple, les
primitives de
. De notre point de vue, il
n'y a donc aucune différence entre les calculs de primitives et les
calculs d'intégrales. Il est courant d'exprimer les primitives des
fonctions usuelles «à une constante près». Par exemple, les
primitives de 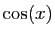 sont toutes les fonctions de la forme
sont toutes les fonctions de la forme
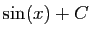 , où
, où 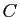 est une constante réelle. Nous écrirons :
est une constante réelle. Nous écrirons :
Or quand 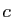 parcourt
parcourt
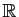 ,
, 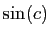 ne prend que les valeurs
comprises entre
ne prend que les valeurs
comprises entre 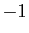 et
et 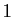 , tandis que
, tandis que 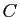 désigne une constante
réelle quelconque. En pratique, il suffit de trouver une primitive
particulière : la variable
désigne une constante
réelle quelconque. En pratique, il suffit de trouver une primitive
particulière : la variable 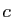 ne sera
qu'un artifice d'écriture. Nous supposerons toujours que
ne sera
qu'un artifice d'écriture. Nous supposerons toujours que 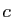 et
et 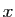 sont telles que la fonction soit définie et continue sur
l'intervalle
sont telles que la fonction soit définie et continue sur
l'intervalle ![$ [c,x]$](img47.gif) . Par exemple :
. Par exemple :
ce qui suppose que l'intervalle ![$ [c,x]$](img47.gif) ne contient pas 0. Dans
cette écriture,
ne contient pas 0. Dans
cette écriture, 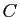 désigne en fait une fonction, qui est constante sur
chaque intervalle où la fonction à intégrer est définie et continue.
L'ensemble des primitives de la fonction
désigne en fait une fonction, qui est constante sur
chaque intervalle où la fonction à intégrer est définie et continue.
L'ensemble des primitives de la fonction
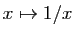 est l'ensemble des fonctions
est l'ensemble des fonctions 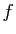 telles que :
telles que :
où 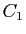 et
et 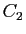 sont deux réels quelconques.
En pratique, pour calculer une primitive d'une fonction donnée, on
la ramène à un catalogue de primitives usuelles. Ces
primitives, que l'on doit connaître, sont rassemblées dans le
tableau ci-dessous. Attention : les intervalles de
définition ne sont pas précisés.
sont deux réels quelconques.
En pratique, pour calculer une primitive d'une fonction donnée, on
la ramène à un catalogue de primitives usuelles. Ces
primitives, que l'on doit connaître, sont rassemblées dans le
tableau ci-dessous. Attention : les intervalles de
définition ne sont pas précisés.
| Fonction |
Une primitive |
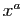 ( (
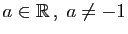 ) ) |
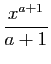 |
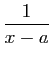 |
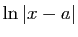 |
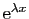 ( (
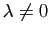 ) ) |
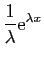 |
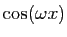 ( (
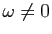 ) ) |
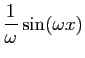 |
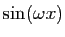 ( (
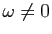 ) ) |
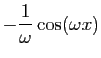 |
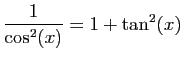 |
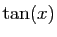 |
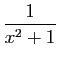 |
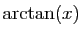 |
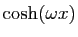 ( (
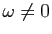 ) ) |
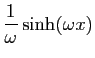 |
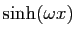 ( (
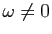 ) ) |
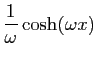 |
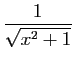 |
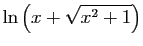 |
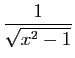 |
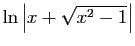 |
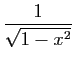 |
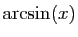 |
Nous rappelons dans la section suivante les techniques de base pour le
calcul des primitives, lorsqu'elles peuvent s'exprimer à
l'aide des fonctions classiques.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
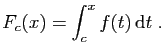
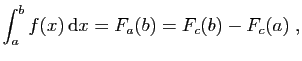
![$\displaystyle \int_a^b f(x) \mathrm{d}x = F_c(b)-F_c(a) = \Big[ F_c(x) \Big]_a^b\;.
$](img38.gif)
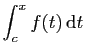 la primitive de
la primitive de ![]() qui s'annule en
qui s'annule en
![]() , même s'il est superflu de fixer
, même s'il est superflu de fixer ![]() . De notre point de vue, il
n'y a donc aucune différence entre les calculs de primitives et les
calculs d'intégrales. Il est courant d'exprimer les primitives des
fonctions usuelles «à une constante près». Par exemple, les
primitives de
. De notre point de vue, il
n'y a donc aucune différence entre les calculs de primitives et les
calculs d'intégrales. Il est courant d'exprimer les primitives des
fonctions usuelles «à une constante près». Par exemple, les
primitives de ![]() sont toutes les fonctions de la forme
sont toutes les fonctions de la forme
![]() , où
, où ![]() est une constante réelle. Nous écrirons :
est une constante réelle. Nous écrirons :
![$\displaystyle \int_c^x \cos(t) \mathrm{d}t = \Big[ \sin(t) \Big]_c^x = \sin(x)-\sin(c) =
\sin(x)+C\;.
$](img43.gif)
![$\displaystyle \int_c^x \frac{1}{t} \mathrm{d}t = \Big[ \ln\vert t\vert\Big]_c^x =
\ln\vert x\vert+C\;,
$](img48.gif)
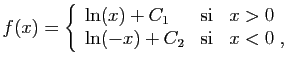
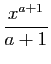
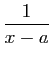
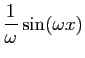
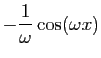
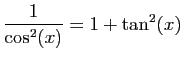
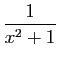
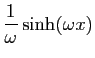
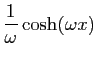
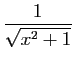
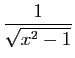
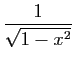
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales