Toutes les fonctions considérées sont supposées
continues, ou continues par morceaux,
sur leur intervalle d'intégration, et sont donc
intégrables. Nous commençons par résumer les principales
propriétés des intégrales.
Théorème 1
- Relation de Chasles :
- Linéarité :
- Monotonie :
Si
![$\displaystyle \forall x\in [a,b] ,\; f(x)\leq g(x)$](img5.gif)
alors
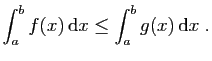
La relation de Chasles permet d'étendre la définition de
l'intégrale au cas où la fonction 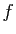 n'est continue que par
morceaux sur l'intervalle d'intégration. On intègre séparément
chacun des morceaux et on ajoute ensuite les intégrales
obtenues. Considérons par exemple la fonction
n'est continue que par
morceaux sur l'intervalle d'intégration. On intègre séparément
chacun des morceaux et on ajoute ensuite les intégrales
obtenues. Considérons par exemple la fonction 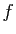 qui vaut
qui vaut 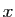 si
si
![$ x\in [0,1]$](img9.gif) et
et
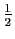 si
si
![$ x\in ]1,2]$](img11.gif) .
.
Figure 1:
Exemple de fonction discontinue.
|
|
Son intégrale sur l'intervalle ![$ [0,2]$](img13.gif) vaut :
vaut :
À propos de cet exemple, il est conseillé de ne pas perdre de vue
l'interprétation géométrique d'une intégrale : l'intégrale
d'une fonction constante positive est la surface d'un rectangle, l'intégrale
d'une fonction affine positive ou nulle
(du type
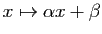 ) est la surface d'un
triangle si la fonction s'annule sur l'une des deux bornes, la surface
d'un trapèze dans le cas général.
) est la surface d'un
triangle si la fonction s'annule sur l'une des deux bornes, la surface
d'un trapèze dans le cas général.
La relation de Chasles reste vraie même si les bornes des
intervalles d'intégration ne sont pas dans le bon ordre, ce qui
peut arriver après un changement de variable. On convient
de changer le signe de l'intégrale quand on échange les
bornes. Cette convention est cohérente avec le fait que
l'intégrale sur un intervalle de longueur nulle vaut
nécessairement 0.
La propriété 2 du théorème (linéarité), dit que
l'intégrale est une application linéaire, de l'espace vectoriel des
fonctions intégrables, dans
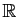 . On l'utilisera souvent, soit pour
mettre en facteur une constante devant l'intégrale, soit pour
séparer le calcul en deux intégrales plus simples. Par exemple :
. On l'utilisera souvent, soit pour
mettre en facteur une constante devant l'intégrale, soit pour
séparer le calcul en deux intégrales plus simples. Par exemple :
On peut utiliser la monotonie pour vérifier certains calculs.
Par exemple si une fonction est positive sur l'intervalle
d'intégration, son intégrale doit être positive. L'intégrale
d'une fonction positive et non identiquement nulle est même
strictement positive : on utilise souvent ce résultat sous la forme
suivante.
L'intégrale peut être
encadrée à l'aide du minimum et du maximum de 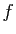 sur l'intervalle
sur l'intervalle
![$ [a,b]$](img19.gif) :
:
Si on divise ces inégalités par la longueur de l'intervalle, on
obtient :
Il faut comprendre
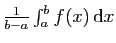 comme la valeur moyenne de la fonction sur l'intervalle.
Le théorème de la moyenne dit que cette valeur moyenne est
atteinte sur l'intervalle.
comme la valeur moyenne de la fonction sur l'intervalle.
Le théorème de la moyenne dit que cette valeur moyenne est
atteinte sur l'intervalle.
Théorème 2
Si  est continue sur
est continue sur ![$ [a,b]$](img19.gif) , il existe
, il existe
![$ c\in [a,b]$](img25.gif) tel que :
tel que :
Figure 2:
Illustration du théorème de la moyenne.
|
|
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
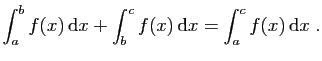
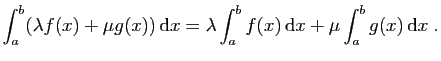
![$\displaystyle \forall x\in [a,b] ,\; f(x)\leq g(x)$](img5.gif) alors
alors 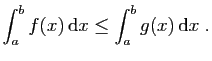
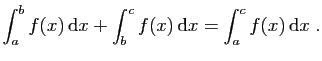
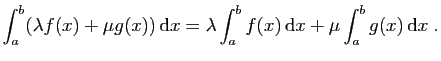
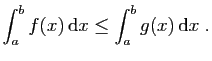
![]() vaut :
vaut :
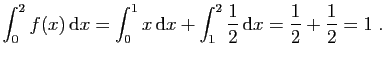
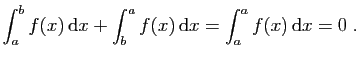

![$\displaystyle \int_a^b \vert f(x)\vert \mathrm{d}x =0 \Longrightarrow f(x)=0 ,\;\forall x\in[a,b]\;.
$](img21.gif)
![$\displaystyle (b-a)\inf_{x\in[a,b]}f(x) \leq \int_a^b f(x) \mathrm{d}x
\leq (b-a)\sup_{x\in[a,b]}f(x) \;.
$](img22.gif)
![$\displaystyle \inf_{x\in[a,b]}f(x) \leq \frac{1}{b-a}\int_a^b f(x) \mathrm{d}x
\leq \sup_{x\in[a,b]}f(x) \;.
$](img23.gif)
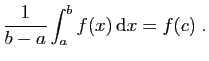
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales