Toute fonction continue sur un intervalle admet une infinité de
primitives sur cet intervalle.
La question du calcul d'une primitive recouvre en fait
deux problèmes très différents. Le premier est celui
du calcul numérique d'une ou plusieurs de ses
valeurs, qui par nature sera une approximation
(l'ordinateur ne peut donner que des résultats décimaux).
L'autre problème est celui du calcul formel,
qui consiste à trouver une expression d'une primitive à
l'aide de fonctions connues.
Considérons par exemple les fonctions suivantes.
Ont-elles une primitive que l'on peut calculer ?
-
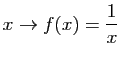
-
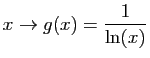 .
.
La réponse est oui pour 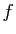 , dont une primitive est
, dont une primitive est
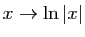 , dans la mesure où on considère
que
, dans la mesure où on considère
que 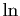 est une fonction connue.
C'est non pour
est une fonction connue.
C'est non pour 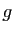 sauf si on définit la fonction
logarithme intégral que l'on note
sauf si on définit la fonction
logarithme intégral que l'on note
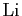 :
:
Cette fonction apparaît naturellement dans des problèmes
pratiques, tout comme le logarithme ordinaire.
De la même façon, on est amené à définir le sinus
intégral, le cosinus intégral, l'exponentielle intégrale.
Encore étudiant, J.W.L. Glaisher (1848-1928) publia un article sur
les fonctions sinus intégral, cosinus intégral et exponentielle
intégrale, contenant des tables de valeurs inédites. Il deviendra
un spécialiste reconnu du calcul de tables numériques.
Au cours du temps, de nombreuses fonctions sont ainsi apparues, et
sont désormais intégrées aux logiciels de calcul. Une des
plus connues est la fonction
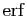 (pour «error function»), très
utilisée en statistique, qui est définie comme suit.
(pour «error function»), très
utilisée en statistique, qui est définie comme suit.
Toutes ces fonctions «spéciales», ont exactement le même statut
mathématique que les fonctions usuelles : on peut les dériver, les
intégrer, les associer à d'autres fonctions dans des formules, etc. Au
moment de calculer numériquement une valeur
particulière, un logiciel de calcul utilisera toujours un
algorithme d'approximation ; mais c'est aussi le cas pour les
fonctions usuelles...
Alors pourquoi distinguer les fonctions spéciales des autres
fonctions ? Peut-être parce que les fonctions usuelles vous posent
déjà suffisamment de problèmes, sans en rajouter !
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
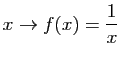
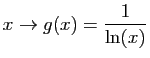 .
.
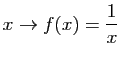
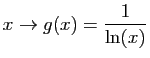 .
.
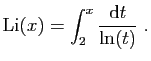
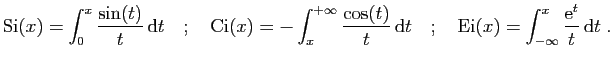
![]() (pour «error function»), très
utilisée en statistique, qui est définie comme suit.
(pour «error function»), très
utilisée en statistique, qui est définie comme suit.
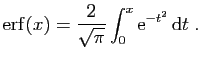
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales