Il y a plus de deux millénaires, Archimède savait
déjà calculer l'aire délimitée par un arc de parabole.
Pourtant, jusqu'au XVIIe siècle, calculer la longueur d'un arc de
courbe fut considéré comme impossible. L'idée qu'un arc de
courbe puisse être mesuré au même titre qu'un segment de droite
semblait même absurde à beaucoup de mathématiciens. Le progrès
vint de l'idée que la longueur d'un arc de courbe puisse être
approchée par celle d'une chaîne de segments ayant leurs
extrémités sur la courbe.
Pierre de Fermat (1601-1665) fut le premier à réaliser que le
calcul d'un arc de courbe se ramenait au calcul de l'aire inscrite
sous une autre courbe, soit en termes modernes, une intégrale.
Pourtant, même après que la méthode de calcul fut comprise,
les tentatives pour calculer la longueur d'un arc d'ellipse
échouèrent.
Voici une des façons d'écrire le problème. Les
équations paramétriques d'une ellipse parallèle aux axes sont :
où 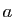 et
et 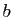 désignent les longueurs du demi-axe horizontal et du
demi-axe vertical (figure 3).
désignent les longueurs du demi-axe horizontal et du
demi-axe vertical (figure 3).
Figure:
Ellipse d'équations paramétriques
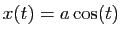 ,
,
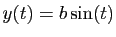 .
.
|
|
La formule pour calculer la longueur d'un arc de courbe paramétrique
entre deux valeurs 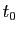 et
et 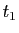 du paramètre est :
du paramètre est :
Ici la longueur de l'arc de courbe compris entre l'axe horizontal et
le rayon d'angle 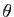 est :
est :
Dans le cas où l'ellipse est un cercle (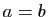 ), il n'y a aucun
problème car la fonction à intégrer est constante. Mais si
), il n'y a aucun
problème car la fonction à intégrer est constante. Mais si
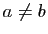 ?
Voici ce que donne le changement de variable
?
Voici ce que donne le changement de variable 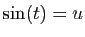 , en posant
, en posant
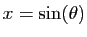 :
:
avec
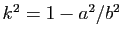 (quitte à effectuer une rotation de
(quitte à effectuer une rotation de 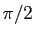 ,
on peut supposer
,
on peut supposer 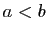 ).
En multipliant en haut et en bas par le numérateur, il
vient :
).
En multipliant en haut et en bas par le numérateur, il
vient :
soit
La seconde de ces deux primitives se calcule grâce à une
intégration par parties. Mais la première ne se calcule pas :
c'est ce qu'on appelle une intégrale elliptique.
Le
premier à s'être posé le problème est Wallis en
1655. Il avait exprimé le résultat sous forme d'une série
entière, et montré que les longueurs d'autres arcs de courbes
conduisaient à des problèmes du même type.
Liouville devait démontrer plus tard que 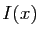 ne s'exprime pas à
l'aide des fonctions usuelles, mais dès la fin du
XVIIIe siècle,
on commence à étudier les propriétés de
ne s'exprime pas à
l'aide des fonctions usuelles, mais dès la fin du
XVIIIe siècle,
on commence à étudier les propriétés de 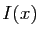 comme une
nouvelle fonction, à l'égal de l'exponentielle et des fonctions
trigonométriques, sans plus chercher à la calculer explicitement.
comme une
nouvelle fonction, à l'égal de l'exponentielle et des fonctions
trigonométriques, sans plus chercher à la calculer explicitement.
Un progrès considérable fut réalisé
indépendamment par Abel et Jacobi en 1826. Ils eurent l'idée, d'une
part de prendre la réciproque de la fonction
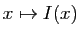 ,
d'autre part d'étendre cette réciproque en une fonction à
valeurs complexes. Cette nouvelle fonction, et ses
généralisations, allaient jouer un rôle important en analyse, en
géométrie et en théorie des nombres. Les généralisations
portent désormais le nom d'intégrales abéliennes, en hommage à
Abel.
,
d'autre part d'étendre cette réciproque en une fonction à
valeurs complexes. Cette nouvelle fonction, et ses
généralisations, allaient jouer un rôle important en analyse, en
géométrie et en théorie des nombres. Les généralisations
portent désormais le nom d'intégrales abéliennes, en hommage à
Abel.
Né en 1802 dans une île proche de Stavanger en Norvège, Niels
Henrik Abel, second fils d'une famille de sept enfants, dut assumer à
18 ans, après le décès de son père, la responsabilité de sa
famille. En plus des leçons particulières qu'il devait donner
pour nourrir les siens, il continua à étudier, et à 20 ans,
il écrivit un mémoire démontrant
l'impossibilité de la résolution d'une équation
du cinquième degré par
radicaux. Avec son travail sur les intégrales elliptiques, il
était déjà à 24 ans, l'auteur de plusieurs résultats
majeurs. Il entreprit alors un tour d'Europe pour rencontrer les
grands mathématiciens du moment. Malheureusement, auprès de Gauss
comme de Cauchy, il se heurta à la négligence et
l'incompréhension. Chargé de présenter les travaux d'Abel à
l'Académie des Sciences, Cauchy commença par égarer
le mémoire. Pressé par
Legendre, il finit par écrire un rapport bâclé, indigne de lui
et de la qualité du travail d'Abel. L'Académie des Sciences ne
rendit justice à Abel qu'en 1830, après sa mort, et il fallut pour
cela une démarche diplomatique de la Norvège.
Découragé et très démuni, Abel mourut en avril 1829
d'une tuberculose pulmonaire avant d'avoir atteint ses 27 ans. Il n'a
jamais su que son nom serait un jour donné à des fonctions,
plusieurs théorèmes importants... et à un
des prix les plus prestigieux en mathématiques.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
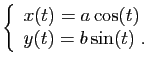
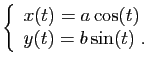
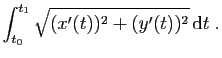
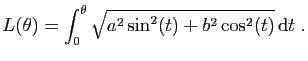
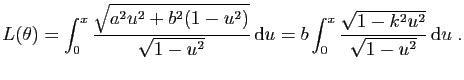
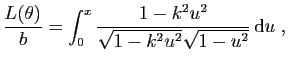
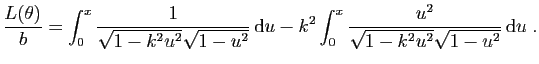
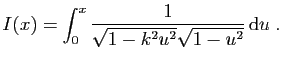
![]() ,
d'autre part d'étendre cette réciproque en une fonction à
valeurs complexes. Cette nouvelle fonction, et ses
généralisations, allaient jouer un rôle important en analyse, en
géométrie et en théorie des nombres. Les généralisations
portent désormais le nom d'intégrales abéliennes, en hommage à
Abel.
,
d'autre part d'étendre cette réciproque en une fonction à
valeurs complexes. Cette nouvelle fonction, et ses
généralisations, allaient jouer un rôle important en analyse, en
géométrie et en théorie des nombres. Les généralisations
portent désormais le nom d'intégrales abéliennes, en hommage à
Abel.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales