Étant donné un cercle, dessiné sur une feuille de papier,
construire en utilisant uniquement une règle et un compas,
un carré dont la surface est égale à celle du cercle.
Tel est l'énoncé du problème dit de «la quadrature du cercle»,
qui a occupé les mathématiciens amateurs et professionnels pendant
tant de siècles, qu'il est devenu dans le langage courant un archétype
de problème insoluble. Effectivement, la quadrature du cercle
est impossible, et la démonstration définitive a été donnée
en 1882 par Carl von Lindemann (1852-1939).
Ceci n'empêche pas de nombreux amateurs peu au fait
des mathématiques d'essayer encore et encore, et de proposer leurs
solutions (fausses bien sûr). Au point que l'Académie des Sciences
a dû déclarer que désormais elle refuserait d'examiner
tout mémoire portant sur la quadrature du cercle.
On peut construire à la règle et au
compas toutes sortes de droites, de cercles et de points.
On peut construire des perpendiculaires et des
parallèles, des médianes, des
médiatrices, des bissectrices...
Qu'est-ce qui distingue ce qui peut être construit à
la règle et au compas de ce qui ne peut pas ? La réponse fut
donnée en 1837 par Pierre-Laurent Wantzel (1814-1848)
(il avait 23 ans).
On appelle nombre constructible toute
coordonnée d'un point que l'on peut
construire à la règle et au compas,
à partir d'un repère
orthonormé donné du plan.
Théorème 6
Tout nombre constructible est racine d'un polynôme à coefficients
entiers, et le plus petit degré d'un polynôme à coefficients
entiers dont ce nombre est racine est une puissance de 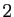 .
.
Wantzel mettait ainsi un point final à deux autres problèmes
célèbres hérités des Grecs : la duplication du cube
(construire un cube de volume double de celui d'un cube donné),
et la trissection de l'angle (construire un angle égal au
tiers d'un angle donné). Mais il ne résolvait pas tout à fait
la quadrature du cercle. Le côté d'un carré dont la surface
est égale à 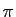 est
est
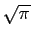 . D'après le théorème de
Wantzel, si
. D'après le théorème de
Wantzel, si
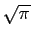 est constructible alors
est constructible alors 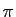 l'est aussi.
Comment prouver que
l'est aussi.
Comment prouver que 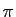 n'est pas constructible ?
Il se trouve que
n'est pas constructible ?
Il se trouve que 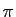 est transcendant, c'est
à dire qu'il n'est racine d'aucun polynôme à coefficients
entiers. Que
est transcendant, c'est
à dire qu'il n'est racine d'aucun polynôme à coefficients
entiers. Que 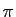 est irrationnel avait déjà été
soupçonné par les Grecs (en particulier Archimède) et
conjecturé après eux par les mathématiciens arabes, notamment Al
Biruni (973-1049) (dont La Fontaine a injustement fait «Aliboron»).
Il fallut attendre Jean-Henri Lambert en 1766 pour la première
démonstration, à base de fractions continues. Du fait de
l'enjeu (la quadrature du cercle), la
transcendance de
est irrationnel avait déjà été
soupçonné par les Grecs (en particulier Archimède) et
conjecturé après eux par les mathématiciens arabes, notamment Al
Biruni (973-1049) (dont La Fontaine a injustement fait «Aliboron»).
Il fallut attendre Jean-Henri Lambert en 1766 pour la première
démonstration, à base de fractions continues. Du fait de
l'enjeu (la quadrature du cercle), la
transcendance de 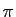 fit l'objet d'une belle compétition entre
mathématiciens, tout au long du XIXe siècle.
Lindemann remporta la palme en 1882, en utilisant la
transcendance de
fit l'objet d'une belle compétition entre
mathématiciens, tout au long du XIXe siècle.
Lindemann remporta la palme en 1882, en utilisant la
transcendance de
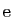 , démontrée avant lui par Charles Hermite.
, démontrée avant lui par Charles Hermite.
La démonstration de Lindemann est beaucoup trop difficile pour être
exposée ici. En utilisant uniquement les outils à
votre disposition, et en particulier les calculs d'intégrales, nous
allons prouver plus modestement l'irrationalité de
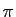 , par une démonstration différente de celle de Lambert.
, par une démonstration différente de celle de Lambert.
Théorème 7
Le nombre 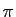 est irrationnel.
est irrationnel.
Démonstration : C'est une démonstration par l'absurde. On suppose
que 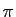 est rationnel, donc qu'il s'écrit
est rationnel, donc qu'il s'écrit 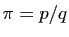 , où
, où 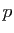 et
et
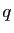 sont deux entiers. Pour tout
sont deux entiers. Pour tout
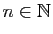 , posons :
, posons :
Observez que 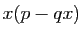 s'annule pour
s'annule pour 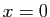 et pour
et pour 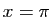 , par
hypothèse. Entre les deux,
, par
hypothèse. Entre les deux, 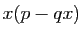 et
et 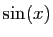 sont strictement
positifs ; donc l'intégrale
sont strictement
positifs ; donc l'intégrale 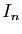 est strictement positive pour tout
est strictement positive pour tout
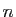 .
.
La démonstration comporte deux étapes. On montre d'abord
que 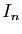 est un entier divisible par
est un entier divisible par 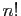 , ensuite que
, ensuite que 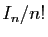 tend
vers 0 quand
tend
vers 0 quand 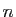 tend vers l'infini. Mais une suite d'entiers qui tend
vers 0 est nulle à partir d'un certain rang. Or
tend vers l'infini. Mais une suite d'entiers qui tend
vers 0 est nulle à partir d'un certain rang. Or 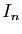 est
strictement positive pour tout
est
strictement positive pour tout 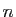 . D'où la contradiction.
. D'où la contradiction.
Étape 1 : 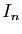 est un multiple entier de
est un multiple entier de 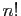 .
.
C'est une démontration par récurrence, pour laquelle il nous faut
une formule du même métal. On l'obtient grâce à deux
intégrations par parties successives.
Pour initialiser la récurrence, calculons 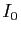 et
et 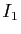 .
.
On calcule 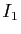 , à nouveau par parties.
, à nouveau par parties.
Donc 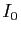 et
et 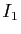 sont entiers (multiples de
sont entiers (multiples de
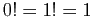 ). L'expression de
). L'expression de 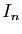 en fonction de
en fonction de 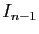 et
et
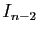 montre que si
montre que si 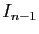 est multiple entier de
est multiple entier de 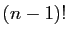 et
et
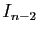 est multiple entier de
est multiple entier de 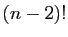 , alors
, alors 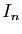 est multiple
entier de
est multiple
entier de 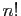 . D'où le résultat, par récurrence.
Étape 2 : La suite
. D'où le résultat, par récurrence.
Étape 2 : La suite 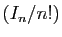 converge vers 0.
converge vers 0.
Le maximum de la fonction
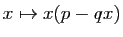 est atteint pour
est atteint pour 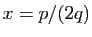 et vaut
et vaut 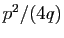 . Donc :
. Donc :
Or pour tout
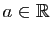 , la suite
, la suite 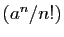 converge vers 0, d'où
le résultat.
converge vers 0, d'où
le résultat. Au passage, ce n'est que depuis le XVIIe siècle que le rapport de
la circonférence d'un cercle à son diamètre se note
Au passage, ce n'est que depuis le XVIIe siècle que le rapport de
la circonférence d'un cercle à son diamètre se note 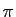 (du
terme grec
(du
terme grec
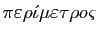 (périmètre), qu'Archimède utilisait pour
désigner la circonférence). Il semble que ce soit
William Oughtred (1574-1660) qui ait le premier utilisé
la notation
(périmètre), qu'Archimède utilisait pour
désigner la circonférence). Il semble que ce soit
William Oughtred (1574-1660) qui ait le premier utilisé
la notation 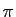 , comme les signes
, comme les signes 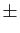 et
et
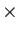 . Il a aussi construit une des premières échelles
logarithmiques, ouvrant ainsi la voie à la règle à calcul.
La lettre
. Il a aussi construit une des premières échelles
logarithmiques, ouvrant ainsi la voie à la règle à calcul.
La lettre 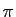 est devenue une notation standard
après les travaux d'Euler
en 1737.
est devenue une notation standard
après les travaux d'Euler
en 1737.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() , par une démonstration différente de celle de Lambert.
, par une démonstration différente de celle de Lambert.
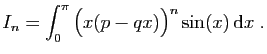
![]() est un entier divisible par
est un entier divisible par ![]() , ensuite que
, ensuite que ![]() tend
vers 0 quand
tend
vers 0 quand ![]() tend vers l'infini. Mais une suite d'entiers qui tend
vers 0 est nulle à partir d'un certain rang. Or
tend vers l'infini. Mais une suite d'entiers qui tend
vers 0 est nulle à partir d'un certain rang. Or ![]() est
strictement positive pour tout
est
strictement positive pour tout ![]() . D'où la contradiction.
. D'où la contradiction.
![]() est un multiple entier de
est un multiple entier de ![]() .
.
![$\displaystyle \Big[\big(x(p-qx)\big)^n(-\cos(x))\Big]_0^\pi
+\int_0^\pi n(p-2qx)\big(x(p-qx)\big)^{n-1}\cos(x) \mathrm{d}x$](img726.gif)
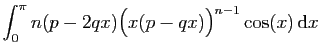
![$\displaystyle \Big[n(p-2qx)\big(x(p-qx)\big)^{n-1}\sin(x)\Big]_0^\pi$](img728.gif)
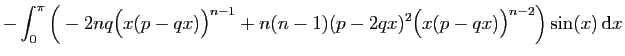
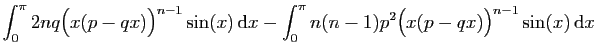
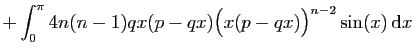
![$\displaystyle I_0=\int_0^\pi \sin(x) \mathrm{d}x=\Big[-\cos(x)\Big]_0^\pi=2\;.
$](img734.gif)
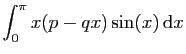
![$\displaystyle \displaystyle{
\Big[x(p-qx)(-\cos(x))\Big]_0^\pi+
\int_0^\pi (p-2qx)\cos(x) \mathrm{d}x}$](img736.gif)
![$\displaystyle \displaystyle{
\Big[(p-2qx)\sin(x)\Big]_0^\pi+
\int_0^\pi 2q\sin(x) \mathrm{d}x=4q\;.}$](img737.gif)
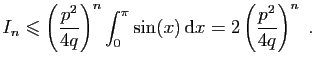
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales