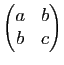 ,
, On a vu à la section 1.1 que toute conique admettait, dans un certain repère orthonormal, une équation polynomiale du second degré. Cette propriété ne dépend en fait pas du repère : si une courbe admet, dans un certain repère cartésien du plan (non nécessairement orthonormé) une équation du second degré, alors elle admet, dans tout repère cartésien du plan, orthonormé ou pas, une équation du second degré.
Soit en effet
![]() , avec
, avec ![]() non tous nuls, l'équation d'une telle courbe
non tous nuls, l'équation d'une telle courbe ![]() dans un certain repère cartésien
dans un certain repère cartésien
![]() et soit
et soit
![]() un autre repère cartésien du plan. Notons
un autre repère cartésien du plan. Notons ![]() (resp.
(resp.![]() ) le vecteur colonne des coordonnées
) le vecteur colonne des coordonnées ![]() (resp.
(resp. ![]() ) d'un point
) d'un point ![]() dans le repère
dans le repère
![]() (resp.
(resp.
![]() ),
), ![]() la matrice
la matrice
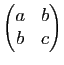 ,
, ![]() le vecteur colonne de composantes
le vecteur colonne de composantes ![]() ,
, ![]() la matrice de passage de la base
la matrice de passage de la base
![]() à la base
à la base
![]() et
et ![]() le vecteur colonne des coordonnées de
le vecteur colonne des coordonnées de ![]() dans le repère
dans le repère
![]() .
.
L'équation de ![]() dans le repère
dans le repère
![]() s'écrit alors
s'écrit alors
![]() . Mais les coordonnées de
. Mais les coordonnées de ![]() dans le repère
dans le repère
![]() sont données par
sont données par ![]() . Il en résulte que l'équation de
. Il en résulte que l'équation de ![]() dans le repère
dans le repère
![]() s'écrit
s'écrit
![]() , soit encore
, soit encore
![]() , où
, où
![]() ,
,
![]() ,
,
![]() . Cette équation est encore polynomiale du second degré en
. Cette équation est encore polynomiale du second degré en ![]() .
.
Le but de cette section est de montrer que, réciproquement, toute courbe plane admettant une équation du second degré est une conique (éventuellement dégénérée) et de ramener son équation, par un changement de repère approprié, à une des formes canoniques obtenues à la section 1.1.
On considère donc dans toute cette section une courbe plane ![]() (éventuellement vide ou réduite à un point) admettant, dans un certain repère orthonormal
(éventuellement vide ou réduite à un point) admettant, dans un certain repère orthonormal
![]() du plan, une équation du second degré, de la forme :
du plan, une équation du second degré, de la forme :
En introduisant comme précédemment la matrice
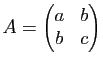 et les matrices colonnes
et les matrices colonnes
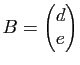 et
et
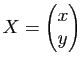 , l'équation de
, l'équation de ![]() dans le repère
dans le repère
![]() s'écrit
s'écrit
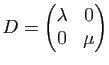 (où
(où 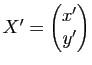 .
L'équation de
.
L'équation de
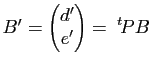 .
Les matrices
.
Les matrices
Premier cas : ![]() .
.
Dans ce cas, ![]() et
et ![]() sont de même signe ; on peut donc, quitte à multiplier l'équation par -1, les supposer tous deux positifs et poser
sont de même signe ; on peut donc, quitte à multiplier l'équation par -1, les supposer tous deux positifs et poser
![]() ,
,
![]() pour des réels positifs
pour des réels positifs ![]() et
et ![]() . L'équation de
. L'équation de ![]() dans le repère
dans le repère
![]() s'écrit alors
s'écrit alors
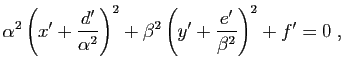
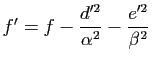 .
.
Soit ![]() le point de coordonnées
le point de coordonnées
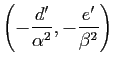 dans le repère
dans le repère
![]() ,
,
![]() le repère
le repère
![]() et
et ![]() les coordonnées dans
les coordonnées dans
![]() d'un point de coordonnées
d'un point de coordonnées ![]() dans
dans
![]() , de sorte que
, de sorte que
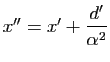 ,
,
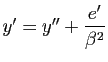 . L'équation de
. L'équation de ![]() dans
dans
![]() s'écrit donc
s'écrit donc
Trois cas se présentent :
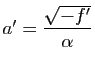 ,
,
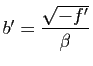 , sous la forme
, sous la forme
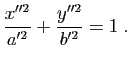
On dit, dans tous ces cas, que ![]() est du genre ellipse.
est du genre ellipse.
Deuxième cas : ![]() .
.
Les deux réels ![]() et
et ![]() sont de signes contraires ; on peut donc, quitte à multiplier l'équation par -1, supposer
sont de signes contraires ; on peut donc, quitte à multiplier l'équation par -1, supposer
![]() et
et ![]() et poser
et poser
![]() ,
,
![]() pour des réels positifs
pour des réels positifs ![]() et
et ![]() . L'équation de
. L'équation de ![]() dans le repère
dans le repère
![]() s'écrit alors
s'écrit alors
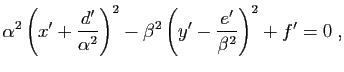
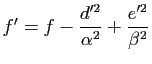 .
.
Soit ![]() le point de coordonnées
le point de coordonnées
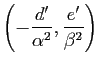 dans le repère
dans le repère
![]() ,
,
![]() le repère
le repère
![]() et
et ![]() les coordonnées dans
les coordonnées dans
![]() d'un point de coordonnées
d'un point de coordonnées ![]() dans
dans
![]() , de sorte que
, de sorte que
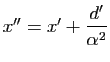 ,
,
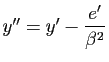 . L'équation de
. L'équation de ![]() dans
dans
![]() s'écrit donc
s'écrit donc
Trois cas se présentent :
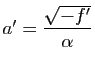 ,
,
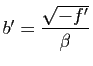 , sous la forme
, sous la forme
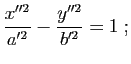
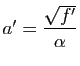 ,
,
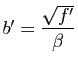 , sous la forme
, sous la forme
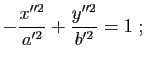
On dit, dans tous ces cas, que ![]() est du genre hyperbole.
est du genre hyperbole.
Troisième cas : ![]() .
.
On a alors
![]() , mais un seul des deux nombres
, mais un seul des deux nombres ![]() et
et ![]() est nul, sinon la matrice
est nul, sinon la matrice ![]() serait nulle et l'équation de
serait nulle et l'équation de ![]() ne serait plus du second degré.
On peut donc supposer
ne serait plus du second degré.
On peut donc supposer ![]() ,
, ![]() . L'équation de
. L'équation de ![]() dans le repère
dans le repère
![]() s'écrit
s'écrit
![]() , soit encore
, soit encore
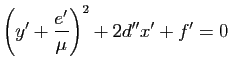
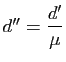 ,
,
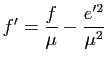 .
.
Quatre cas se présentent :
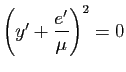 ;
; 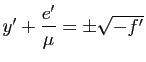 ;
;
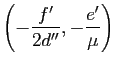 dans le repère
dans le repère
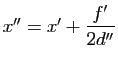 ,
,
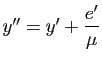 ; l'équation de
; l'équation de
On dit, dans tous ces cas, que ![]() est du genre parabole.
est du genre parabole.
En résumé, on voit que toute courbe admettant une équation polynomiale du second degré est soit une conique ou un cercle, soit vide ou réduite à un point, soit réunion de deux droites, éventuellement confondues. Dans ce dernier cas, l'équation de ![]() se décompose en produit de deux équations du premier degré : on dit que la conique est dégénérée.
se décompose en produit de deux équations du premier degré : on dit que la conique est dégénérée.
|
Recherche d'un centre
En pratique, il est souvent intéressant de commencer par chercher si la conique possède un centre de symétrie et de déterminer, s'il existe, ce centre.
Un point ![]() , de coordonnées
, de coordonnées ![]() dans
dans
![]() , est centre de symétrie de
, est centre de symétrie de ![]() si et seulement si l'équation de
si et seulement si l'équation de ![]() dans le repère
dans le repère
![]() ne comporte pas de termes du premier degré. Les coordonnées
ne comporte pas de termes du premier degré. Les coordonnées ![]() dans
dans
![]() du point
du point ![]() de coordonnées
de coordonnées ![]() dans
dans
![]() sont données par
sont données par ![]() ,
, ![]() . L'équation de
. L'équation de ![]() dans
dans
![]() s'écrit donc :
s'écrit donc :
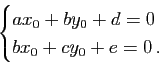
Cette situation se retrouve dans le cas particulier où l'une de ces deux équations n'est pas celle d'une droite :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales