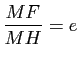 , où
, où
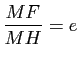 , où
, où
Démonstration : Soit ![]() un point de la conique,
un point de la conique, ![]() la symétrie orthogonale d'axe
la symétrie orthogonale d'axe ![]() ,
, ![]() . Le point
. Le point ![]() est fixe par
est fixe par ![]() et la droite
et la droite ![]() globalement invariante par
globalement invariante par ![]() . Une symétrie orthogonale conserve les distances et l'orthogonalité. Il en résulte que le projeté orthogonal de
. Une symétrie orthogonale conserve les distances et l'orthogonalité. Il en résulte que le projeté orthogonal de ![]() sur
sur ![]() est l'image
est l'image ![]() du projeté orthogonal
du projeté orthogonal ![]() de
de ![]() sur
sur ![]() et que
et que ![]() ,
, ![]() . Le point
. Le point ![]() appartient donc à la conique.
appartient donc à la conique.![]()
Dans le cas particulier où ![]() , la parabole de directrice
, la parabole de directrice ![]() et de foyer
et de foyer ![]() est l'ensemble des points du plan équidistants de la droite
est l'ensemble des points du plan équidistants de la droite ![]() et du point
et du point ![]() ; on peut aussi décrire cet ensemble comme le lieu des centres des cercles tangents à
; on peut aussi décrire cet ensemble comme le lieu des centres des cercles tangents à ![]() passant par
passant par ![]() .
.
![\includegraphics[width=0.5\textwidth]{parabole1}](img19.gif)
La figure GeoGebra illustre cette propriété. Vous pouvez déplacer le point ![]() sur la parabole.
sur la parabole.
Équations réduites
Nous allons chercher dans ce paragraphe un repère dans lequel l'équation de la conique soit la plus simple possible. Une telle équation sera appelée équation réduite de la conique.
La proposition 1 nous amène à travailler dans un repère orthonormal dont l'axe des ![]() est l'axe focal. Soit donc
est l'axe focal. Soit donc
![]() un tel repère,
un tel repère, ![]() les coordonnées de
les coordonnées de ![]() ,
, ![]() l'équation de
l'équation de ![]() dans ce repère. L'équation
dans ce repère. L'équation
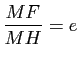 équivaut à
équivaut à
![]() , soit encore :
, soit encore :
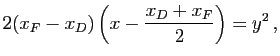
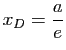 ,
,
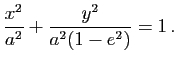
Une symétrie centrale étant une isométrie, on en déduit (démonstration analogue à celle de la proposition 1) pour ces coniques l'existence d'un second couple foyer-directrice ![]() , symétrique du premier par rapport au point
, symétrique du premier par rapport au point ![]() (ou par rapport à l'axe
(ou par rapport à l'axe ![]() ).
).
On est ensuite amené à séparer les cas ![]() et
et ![]() :
:
![]() Si
Si ![]() (cas de l'ellipse), l'axe
(cas de l'ellipse), l'axe ![]() coupe la conique en deux points
coupe la conique en deux points ![]() et
et ![]() , d'ordonnées
, d'ordonnées
![]() . On pose
. On pose
![]() , de sorte que
, de sorte que ![]() . L'équation de l'ellipse s'écrit alors :
. L'équation de l'ellipse s'écrit alors :
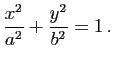
L'ellipse est une courbe bornée : elle est tout entière contenue dans le rectangle de sommets de coordonnées
![]() et est en particulier comprise entre ses deux directrices.
et est en particulier comprise entre ses deux directrices.
![]() Si
Si ![]() (cas de l'hyperbole), l'axe
(cas de l'hyperbole), l'axe ![]() ne coupe pas la conique. On pose
ne coupe pas la conique. On pose
![]() . L'équation de l'hyperbole s'écrit alors :
. L'équation de l'hyperbole s'écrit alors :
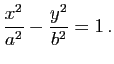
![\includegraphics[width=0.45\textwidth]{ellipse}](img76.gif)
![\includegraphics[width=0.45\textwidth]{hyperbole}](img77.gif)
Une parabole ou une ellipse sépare le plan en deux régions, définies par les inégalités ![]() et
et ![]() . Une hyperbole sépare le plan en trois régions, dont deux correspondent à l'inégalité
. Une hyperbole sépare le plan en trois régions, dont deux correspondent à l'inégalité ![]() et une (celle située en les deux branches) à l'inégalité
et une (celle située en les deux branches) à l'inégalité ![]() .
.
Remarque : on peut considérer le cercle d'équation
![]() , de centre
, de centre ![]() et de rayon
et de rayon ![]() , comme un cas limite d'ellipse, pour lequel
, comme un cas limite d'ellipse, pour lequel ![]() ,
, ![]() ,
, ![]() , les directrices étant repoussées à l'infini et les deux foyers confondus. Il n'est néanmoins pas possible de donner une définition du cercle par foyer et directrice dans le cadre du plan affine euclidien.
, les directrices étant repoussées à l'infini et les deux foyers confondus. Il n'est néanmoins pas possible de donner une définition du cercle par foyer et directrice dans le cadre du plan affine euclidien.
La figure GeoGebra illustre la variation de forme de la conique en fonction de son excentricité. Elle représente une ellipse, une parabole et une hyperbole ayant même foyer ![]() et même directrice
et même directrice ![]() . Vous pouvez en déplaçant les curseurs faire varier l'excentricité de l'ellipse et de l'hyperbole.
. Vous pouvez en déplaçant les curseurs faire varier l'excentricité de l'ellipse et de l'hyperbole.
Représentation paramétrique
Parabole
La parabole d'équation ![]() admet la représentation paramétrique :
admet la représentation paramétrique :
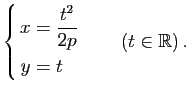 |
Ellipse : L'ellipse d'équation
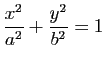 admet la représentation paramétrique :
admet la représentation paramétrique :
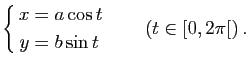 |
Hyperbole : L'hyperbole d'équation
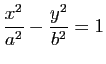 admet la représentation paramétrique :
admet la représentation paramétrique :
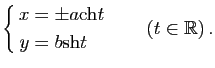 |
Elle admet aussi la représentation paramétrique :
![$\displaystyle \left\{ \begin{aligned}x&=\dfrac{a}{\cos t}\\ y&=b\tan t \end{ali...
...{3\pi}{2}} \right[ \cup \left] \dfrac{\pi}{2},\dfrac{3\pi}{2}\right[\right)\, ,$](img89.gif) |
Elle admet également la représentation paramétrique rationnelle :
![$\displaystyle \left\{ \begin{aligned}x&=\dfrac{a}{2}\left( u+\dfrac{1}{u}\right...
...nd{aligned} \right. \qquad \left(u\in ] -\infty,0[ \cup ] 0,+\infty[\right)\, ,$](img90.gif) |
On en déduit que l'hyperbole d'équation
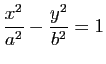 admet deux asymptotes d'équations
admet deux asymptotes d'équations
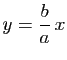 et
et
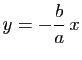 . En effet, en utilisant par exemple la représentation paramétrique
. En effet, en utilisant par exemple la représentation paramétrique ![]() ,
, ![]() de la branche de droite de l'hyperbole, on voit que, pour tout point
de la branche de droite de l'hyperbole, on voit que, pour tout point ![]() de l'hyperbole,
de l'hyperbole,
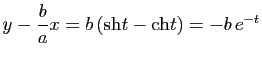 tend vers 0 quand
tend vers 0 quand ![]() tend vers
tend vers ![]() et
et
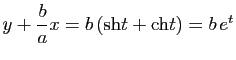 tend vers 0 quand
tend vers 0 quand ![]() tend vers
tend vers ![]() .
.
Équation polaire d'une conique de foyer l'origine
Les lois de Kepler (voir section 3.3) disent que les trajectoires des planètes sont approximativement des ellipses dont le soleil occupe un des foyers. La démonstration de ce résultat fait intervenir l'équation polaire d'une conique dont un des foyers est situé à l'origine du repère. C'est ce qui fait l'importance de la proposition suivante.
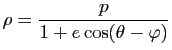
Démonstration : La droite d'équation normale
![]() se déduit de la droite d'équation
se déduit de la droite d'équation ![]() (qui correspond au cas
(qui correspond au cas ![]() ) par la rotation de centre
) par la rotation de centre ![]() et d'angle
et d'angle ![]() . Il suffit donc de faire la démonstration dans le cas où
. Il suffit donc de faire la démonstration dans le cas où ![]() , le cas général se déduit en remplaçant l'angle polaire
, le cas général se déduit en remplaçant l'angle polaire ![]() d'un point
d'un point ![]() par
par
![]() dans l'équation obtenue.
dans l'équation obtenue.
Les coordonnées cartésiennes de ![]() sont alors
sont alors
![]() ,
,
![]() et celles du projeté orthogonal
et celles du projeté orthogonal ![]() de
de ![]() sur
sur ![]()
![]() . La relation
. La relation
![]() s'écrit alors
s'écrit alors
![]() , soit en développant :
, soit en développant :
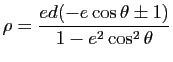
On trouve donc a priori deux courbes d'équations polaires
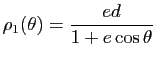 et
et
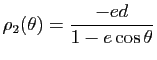 . Mais
. Mais
![]() , ce qui signifie que le point d'angle polaire
, ce qui signifie que le point d'angle polaire
![]() de la première courbe se confond avec le point de paramètre
de la première courbe se confond avec le point de paramètre ![]() de la première. Il suffit donc de garder la première équation.
de la première. Il suffit donc de garder la première équation.![]()
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales