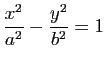Hyperbole rapportée à ses asymptotes

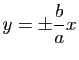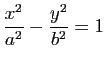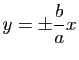L'hyperbole d'équation $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ dans un repère orthonormal $\mathcal R=(O,\vec{i},\vec{j})$ admet comme asymptotes les droites d'équations $y=\pm\dfrac{b}{a} x$ .

Son équation s'écrit encore

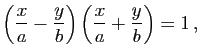
$\displaystyle \left(\dfrac{x}{a}-\dfrac{y}{b}\right) \left(\dfrac{x}{a}+\dfrac{y}{b}\right)=1\, ,$

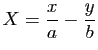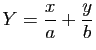soit, en posant $X=\dfrac{x}{a}-\dfrac{y}{b}$ et $Y=\dfrac{x}{a}+\dfrac{y}{b}$ :

$\displaystyle XY=1 \, .$

Mais les relations

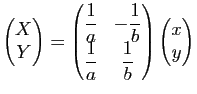
$\displaystyle \begin{pmatrix}X\\ Y\end{pmatrix} = \begin{pmatrix}\dfrac{1}{a}&-... ...}{b}\\ \dfrac{1}{a}&\dfrac{1}{b}\end{pmatrix} \begin{pmatrix}x\\ y\end{pmatrix}$

d'où

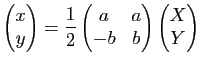
$\displaystyle \begin{pmatrix}x\\ y\end{pmatrix} = \dfrac{1}{2} \begin{pmatrix}a & a\\ -b & b\end{pmatrix} \begin{pmatrix}X\\ Y\end{pmatrix}$

montrent que

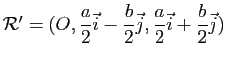sont les coordonnées dans le repère (non orthonormé) $\mathcal R'=(O,\dfrac{a}{2}\vec{i}-\dfrac{b}{2}\vec{j}, \dfrac{a}{2}\vec{i}+\dfrac{b}{2}\vec{j})$ du point de coordonnées

dans le repère $\mathcal R$ . L'équation

est donc celle de l'hyperbole dans ce repère $\mathcal R'$ porté par les asymptotes.

Proposition 9 Pour toute hyperbole , il existe un repère cartésien porté par les asymptotes de dans lequel l'équation de est .

Plus généralement, une hyperbole admet, dans tout repère cartésien porté par ses asymptotes, une équation de la forme , pour un réel non nul.

Un tel repère n'est en général pas orthogonal. Il l'est si et seulement si l'hyperbole est équilatère.

Définition 3 Une hyperbole est dite équilatère si ses asymptotes sont perpendiculaires.

Proposition 10 Une hyperbole est équilatère si et seulement si son excentricité est égale à $\sqrt 2$ .

Démonstration : Les asymptotes de l'hyperbole d'équation 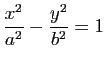$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ dans un repère orthonormal admettent comme vecteurs directeurs les vecteurs et . Ces vecteurs sont orthogonaux si et seulement si , ou encore $c^2=2 \, a^2$ , puisque la demi-distance focale vérifie . Mais l'excentricité est égale à . $\square$

Intersection de l'hyperbole et d'une droite

En utilisant l'équation de l'hyperbole dans un repère porté par les asymptotes, on vérifie immédiatement que toute droite parallèle à l'une des asymptotes (et distincte de cette asymptote) coupe l'hyperbole en exactement un point. Une telle droite admet en effet dans ce repère une équation de la forme ou , où (resp. ) est un réel non nul.

Proposition 11 Si une droite non parallèle aux asymptotes coupe l'hyperbole en deux points et (distincts ou confondus) et les asymptotes en deux points et , les segments et ont même milieu.

Démonstration : Rapportons le plan à un repère (en général non orthonormé) porté par les asymptotes dans lequel l'équation de l'hyperbole est . Une droite non parallèle aux asymptotes a une équation de la forme , avec $uv\not =0$ . Un point de coordonnées appartient à l'hyperbole et à si et seulement si et . La droite coupe donc l'hyperbole en deux points distincts et si le discriminant $w^2-4\, uv$ de cette équation du second degré est strictement positif et un un point double s'il est nul. 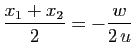Dans le cas où coupe l'hyperbole en deux points distincts ou confondus et , le milieu du segment a pour abscisse $\dfrac{x_1+x_2}{2}=-\dfrac{w}{2\, u}$ . 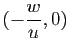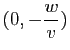Les points et d'intersection de avec les axes ont pour coordonnées $(-\dfrac{w}{u},0)$ et $(0,-\dfrac{w}{v})$ . Les milieux des segments et ont donc même abscisse et sont donc confondus, puisqu'ils appartiennent tous deux à . $\square$

Construction de l'hyperbole point par point

On en déduit une construction point par point d'une hyperbole dont on connaît les asymptotes et un point : si est le point donné, on mène par une droite coupant les asymptotes en et , le symétrique de par rapport au milieu du segment appartient alors à l'hyperbole. On peut ainsi construire à la règle et au compas autant de points de l'hyperbole qu'on le souhaite.

$\includegraphics[width=0.5\textwidth]{construction_hyperbole1}$