Le théorème de Pascal (dit aussi hexagramme mystique de Pascal) dit que si les côtés opposés d'un hexagone inscrit dans une conique se coupent en des points ![]() ,
, ![]() ,
, ![]() , les trois points
, les trois points ![]() ,
, ![]() ,
, ![]() sont alignés.
sont alignés.
![\includegraphics[width=0.8\textwidth]{hexagramme}](img701.gif)
La figure GeoGebra illustre ce théorème. Vous pouvez déformer la conique en déplaçant les cinq points ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() qui la définissent et déplacer le point
qui la définissent et déplacer le point ![]() sur la conique passant par ces cinq points.
sur la conique passant par ces cinq points.
Une conséquence en est que, par cinq points en position générale, il passe une conique et une seule. Le théorème de Pascal donne précisément un moyen de construire point par point cette conique : si ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() sont les points donnés, pour construire un point supplémentaire
sont les points donnés, pour construire un point supplémentaire ![]() de la conique, il suffit de tracer une droite
de la conique, il suffit de tracer une droite ![]() passant par
passant par ![]() ; si les droites
; si les droites ![]() et
et ![]() se coupent en
se coupent en ![]() , les droites
, les droites ![]() et
et ![]() en
en ![]() , et les droites
, et les droites ![]() et
et ![]() en
en ![]() , le point d'intersection
, le point d'intersection ![]() des droites
des droites ![]() et
et ![]() appartient à la conique (en supposant bien sûr ces droites sécantes).
appartient à la conique (en supposant bien sûr ces droites sécantes).
Ce théorème a été énoncé par Blaise Pascal (1623-1662) dans son Essai pour les coniques, composé avant qu'il ait atteint l'âge de dix-sept ans et publié à Paris en février 1640. La démonstration originale de Pascal n'est pas connue dans sa totalité, mais l'idée essentielle en est qu'il suffit de démontrer le théorème pour le cercle. En effet, on peut passer du cercle à n'importe quelle conique par une transformation géométrique simple qui préserve le concours des droites et l'alignement des points. Cette idée, développée par Girard Desargues (1591-1661) dans son Brouillon Project d'une Atteinte aux Evènemens des Rencontres du Cone avec un Plan, paru en 1639, permet de considérer que, du point de vue de la géométrie projective (la partie de la géométrie qui traite justement des propriétés de concours et d'alignement), toutes les coniques sont équivalentes, et repose sur la remarque suivante : si on considère deux sections planes d'un même cône de révolution, on peut établir une correspondance naturelle de l'une sur l'autre en associant à tout point de la première le point de la seconde situé sur la même génératrice du cône.
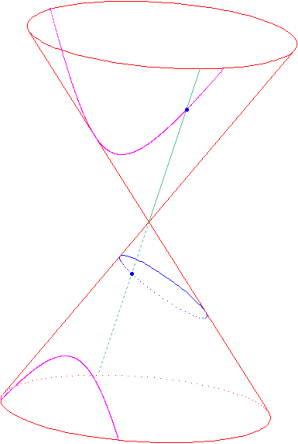
Dans le cas où trois des points donnés (et trois seulement) sont alignés, la conique passant par les cinq points est dégénérée : il s'agit de la réunion des deux droites portant les cinq points.
De fait, dans le cas où la conique dégénère en la réunion de deux droites, le théorème de Pascal se réduit au théorème de Pappus :
![\includegraphics[width=0.6\textwidth]{pappus}](img705.gif)
La figure GeoGebra illustre ce théorème. Vous pouvez déplacer les deux droites en déplaçant les points ![]() ,
, ![]() ,
, ![]() ,
, ![]() et déplacer les points
et déplacer les points ![]() et
et ![]() sur ces deux droites.
sur ces deux droites.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales