Section : Entraînement
Avant : Devoir
Après : Compléments

Corrigé du devoir

Questions de cours :  
  1. La conique $ C$ de foyer $ F$, de directrice $ D$ et d'excentricité $ e>0$, où $ F$ est un point du plan n'appartenant pas à $ D$, est l'ensemble des points du plan dont le rapport $ \dfrac{MF}{MH}$ (où $ H$ est le projeté orthogonal de $ M$ sur $ D$) des distances à $ F$ et à $ D$ est égal à $ e$ :

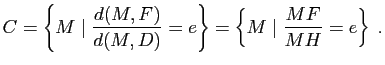
    $\displaystyle C=\left\{ M \mid \dfrac{d(M,F)}{d(M,D)}=e\right\}=\left\{ M \mid \dfrac{MF}{MH}=e\right\} \; .$

  2. Les coniques admettant deux couples foyer-directrice sont les ellipses et les hyperboles.

    Une ellipse $ E$ de foyers $ F$ et $ F'$ est l'ensemble des points $ M$ du plan dont la somme $ MF+MF'$ des distances à ses deux foyers est une constante $ 2a$ strictement supérieure à la distance focale $ FF'$ :

    $\displaystyle E=\{M \mid MF+MF'=2a\}$    avec $\displaystyle 2a>FF'\; .$

    Une hyperbole $ H$ de foyers $ F$ et $ F'$ est l'ensemble des points $ M$ du plan dont la différence $ MF-MF'$ des distances à ses deux foyers est égale en valeur absolue à une constante $ 2a$ strictement inférieure à la distance focale $ FF'$ :

    $\displaystyle H=\{M \mid \vert \, MF-MF'\,\vert=2a\}$    avec $\displaystyle 2a<FF' \; .$

  3. Une hyperbole est dite équilatère si ses asymptotes sont perpendiculaires. Une condition nécessaire et suffisante pour qu'une hyperbole soit équilatère est que son excentricité soit égale à $ \sqrt{2}$.

    L'hyperbole d'équation 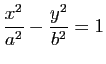$ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ admet comme asymptotes les droites d'équations 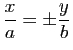$ \dfrac{x}{a}=\pm \dfrac{y}{b}$. Si le repère est orthonormé, elle est équilatère si et seulement si $ a=b$.

  4. L'équation $ ax^2+2bxy+cy^2+2dx+2ey=0$ en repère orthonormal est celle d'un cercle si et seulement si $ a=c\not =0$ et $ b=0$. On remarque que l'ensemble des points vérifiant cette équation n'est jamais vide puisqu'il contient l'origine (ce cercle est réduit à un point si $ d=e=0$).

  5. La courbe d'équation $ x^2-y^2=1$ dans un repère orthonormal est une hyperbole équilatère de centre l'origine, d'axe focal l'axe $ Ox$ et d'asymptotes les bissectrices des axes.

    Elle admet les représentations paramétriques

    $ \bullet$
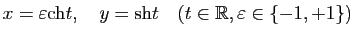    $ x=\varepsilon\ch {t}, \quad y=\sh {t} \quad (t\in\mathbb{R},\varepsilon\in\{-1,+1\})$ ;
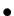
    $ \bullet$
    $ x=\dfrac{1}{\cos t}, \quad y=\tan t \quad \left( t\in \left] -\dfrac{\pi}{2},\... ...ac{3\pi}{2}} \right[ \cup \left] \dfrac{\pi}{2},\dfrac{3\pi}{2}\right[ \right)$ ;
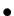
    $ \bullet$
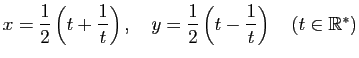    $ x=\dfrac{1}{2}\left(t+\dfrac{1}{t}\right), \quad y=\dfrac{1}{2}\left(t-\dfrac{1}{t}\right) \quad (t\in\mathbb{R}^*)$.

Exercice 1 :  
  1. L'axe $ Ox$ est axe de symétrie pour $ P$, puisque si le point $ (x,y)$ appartient à $ P$, le point $ (x,-y)$ appartient aussi à $ P$.

    Il en résulte que le sommet de $ P$ est l'origine $ O$ du repère.

    Le foyer $ F$ a donc comme coordonnées $ (c,0)$ pour un réel $ c$ et la directrice $ D$ comme équation $ x=-c$. Un point $ M$ de coordonnées $ (x,y)$ appartient à $ P$ si et seulement si $ MF=MH$, où $ H$ est le projeté orthogonal de $ M$ sur $ D$, i.e. le point de coordonnées $ (-c,y)$, d'où l'équation de $ P$ : $ (x-c)^2+y^2=(x+c)^2$, soit encore $ y^2=4cx$. En identifiant cette équation à celle de $ P$, on obtient $ c=p/2$, d'où les coordonnées de $ F$ $ (p/2,0)$ et l'équation de $ D$ : $ x=-p/2$.

  2. Le vecteur dérivé $ (t/p,1)$ du vecteur $ (t^2/2p,t)$ est un vecteur directeur de la tangente à $ P$ au point de paramètre $ t$. Une équation de cette tangente est donc :

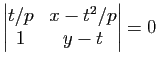
    $\displaystyle \begin{vmatrix} t/p &x-t^2/p\\ 1 & y-t \end{vmatrix}=0$

    ou encore

    $\displaystyle 2ty-2px-t^2=0\; .$

  3. La tangente à $ P$ au point de paramètre $ t$ passe par $ M_0$ si et seulement si

    $\displaystyle t^2-2ty_0+2px_0=0 \; . \qquad \qquad (*)$

    Cette équation du second degré en $ t$ admet des solutions réelles si et seulement si son discriminant réduit $ \Delta '=y_0^2-2px_0$ est positif ou nul. Si $ \Delta'=0$, le point $ M_0$ appartient à $ P$ et l'unique solution de l'équation est $ t=y_0$, ce qui traduit le fait que cette droite est la tangente à $ P$ en $ M_0$.

    Si $ \Delta'>0$, le point $ M_0$ est situé à l'extérieur de la parabole $ P$ (en convenant d'appeler intérieur de la parabole la partie convexe du plan délimitée par celle-ci et extérieur son complémentaire) et il passe par $ M_0$ deux tangentes à $ P$.

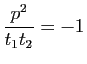
  4. Pour qu'il passe par $ M_0$ deux tangentes à $ P$ perpendiculaires, il faut que $ \Delta'$ soit strictement positif et que le produit des pentes des tangentes à $ P$ passant par $ M_0$ soit égal à 1, i.e. que $ \dfrac{p^2}{t_1t_2}=-1$, où $ t_1$ et $ t_2$ sont les deux racines de $ (*)$. Or $ t_1t_2=2px_0$, d'où la condition $ x_0=-p/2$. Si cette condition est vérifiée, on a $ \Delta'>0$ et il passe donc bien par $ M_0$ deux tangentes à $ P$. Il en résulte que l'ensemble des points d'où l'on peut mener à $ P$ deux tangentes perpendiculaires entre elles est la directrice $ D$ de $ P$.

  5. On sait que la tangente en $ M$ à $ P$ est la médiatrice du segment $ [FH]$ (proposition 4). Tout point de cette tangente est donc équidistant de $ F$ et $ H$.

    On pouvait aussi redémontrer ce résultat : le point $ F$ a pour coordonnées $ (p/2,0)$ et le point $ H$ $ (-p/2,t)$ ; il en résulte que la médiatrice de $ [FH]$ a pour équation

    $\displaystyle (x-p/2)^2+y^2=(x+p/2)^2+(y-t)^2$

    soit encore

    $\displaystyle 2ty-2px-t^2=0$

    qui est l'équation de la tangente en $ M$ à $ P$.

  6. Si un point $ M_0$ du plan appartient à la tangente en $ M$ à $ P$, le cercle de centre $ M_0$ et de rayon $ M_0F$ coupe $ D$ en $ H$. Pour construire les tangentes à $ P$ passant par $ M_0$, il suffit donc de tracer le cercle de centre $ M_0$ et de rayon $ M_0F$. Si ce cercle ne coupe pas $ D$, il ne passe pas par $ M_0$ de tangente à $ P$ (cette condition équivaut à $ d(M_0,D)>M_0F$ et signifie que $ M_0$ est à l'intérieur de la parabole). S'il coupe $ D$ en un unique point $ H$, le point $ M_0$ appartient à $ P$ et la tangente à $ P$ en $ M_0$ est l'unique tangente à $ P$ passant par $ M_0$. S'il coupe $ D$ en deux points distincts $ H_1$ et $ H_2$, on construit deux points $ M_1$ et $ M_2$ de $ P$ en prenant l'intersection de la médiatrice de $ [FH_i]$ avec la perpendiculaire à $ D$ en $ H_i$, et les tangentes à $ P$ en $ M_1$ et $ M_2$ sont les deux tangentes à $ P$ passant par $ M_0$.

    \includegraphics[width=0.7\textwidth]{tangentesparabole}

  7. Les tangentes à $ P$ menées par $ M_0$ sont donc les médiatrices des segments $ [FH_1]$ et $ [FH_2]$, où $ H_1$ et $ H_2$ sont les points d'intersection du cercle $ C$ de centre $ M_0$ passant par $ F$ avec $ D$. Ces deux tangentes sont perpendiculaires si et seulement si les droites $ (FH_1)$ et $ (FH_2)$ le sont, ce qui signifie que le point $ F$ appartient au cercle de diamètre $ [H_1H_2]$. Mais ce cercle n'est autre que $ C$, puisqu'il passe par les trois points $ F$, $ H_1$ et $ H_2$. Son centre $ M_0$ est le milieu de $ [H_1H_2]$ et appartient donc à $ D$. Réciproquement, si $ M_0$ appartient à $ D$, il ressort immédiatement de la construction précédente qu'il passe par $ M_0$ deux tangentes à $ P$ perpendiculaires entre elles. La directrice est ce qu'on appelle la courbe orthoptique de la parabole (ensemble des points d'où l'on voit la parabole sous un angle droit).

    \includegraphics[width=0.7\textwidth]{orthoptiqueparabole}

Exercice 2 :

  1. Le point $ M$ de coordonnées $ (x,y)$ appartient à $ H$ si et seulement si $ MF^2=2d(M,D)^2$, i.e.si et seulement si $ (x-3)^2+(y-2)^2=(x-y+1)^2$, ou encore $ xy-4x-y+6=0$.

  2. Cette équation s'écrit encore $ (x-1)(y-4)=-2$, soit, en posant $ X=x-1$, $ Y=y-4$, $ XY=-2$. Mais $ (X,Y)$ sont les coordonnées du point $ M$ dans le repère $ (\Omega,\vec{i},\vec{j})$, où $ \Omega$ est le point de coordonnées $ (1,4)$ dans le repère initial $ (O,\vec{i},\vec{j})$. L'équation de $ H$ dans ce nouveau repère est donc $ XY=-2$, ce qui montre que la symétrie centrale de centre $ \Omega$ laisse $ H$ invariante. On en déduit que $ \Omega$ est le centre de l'hyperbole $ H$.

  3. Le foyer $ F'$ (resp. la directrice associée $ D'$) est symétrique de $ F$ (resp. de $ D$) par rapport à $ \Omega$. La symétrie centrale de centre $ \Omega$ est donnée par les formules $ x'=2-x$, $ y'=8-y$, où $ (x,y)$ sont les coordonnées d'un point et $ (x',y')$ celles de son image. Il en résulte que $ F'$ a pour coordonnées dans le repère initial $ (-1,6)$ et $ D'$ pour équation dans ce repère $ y-x-5=0$.

  4. La courbe $ E$ d'équation $ 3x^2+3y^2+2xy-14x-26y+27=0$ est une conique du genre ellipse, puisque la forme quadratique $ (x,y)\mapsto 3x^2+3y^2+2xy$ est définie positive. Cette courbe n'est pas vide, puisqu'elle possède par exemple deux points d'abscisse 0, et ce n'est pas un cercle ; c'est donc une ellipse.

  5. Les coordonnées du centre de $ E$ sont solution du système

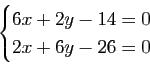
    \begin{displaymath}\begin{cases} 6x+2y-14=0\\ 2x+6y-26=0 \end{cases}\end{displaymath}

    obtenu en annulant les dérivées partielles de $ 3x^2+3y^2+2xy-14x-26y+27$. Ce système admet l'unique solution $ x=1$, $ y=4$.

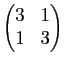
  6. En utilisant les formules de changement de repère $ x=X+1$, $ y=Y+4$, on voit que $ E$ admet comme équation $ 3X^2+3Y^2+2XY-32=0$ dans le repère $ (\Omega,\vec{i},\vec{j})$. Des vecteurs propres de la matrice $ \begin{pmatrix} 3 & 1\\ 1 & 3 \end{pmatrix}$ sont $ (1,1)$ et $ (1,-1)$. 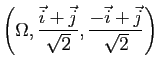Les coordonnées $ (X,Y)$ d'un point $ M$ dans le repère $ (\Omega,\vec{i},\vec{j})$ sont reliées aux coordonnées $ (X',Y')$ de ce point dans le repère orthonormal $ \left(\Omega, \dfrac{\vec{i}+\vec{j}}{\sqrt{2}}, \dfrac{-\vec{i}+\vec{j}}{\sqrt{2}}\right)$ déduit par rotation de centre $ \Omega$ et d'angle $ \pi/4$ par

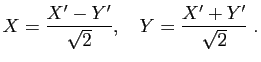
    $\displaystyle X=\dfrac{X'-Y'}{\sqrt{2}},\quad Y=\dfrac{X'+Y'}{\sqrt{2}} \; .$

    Il en résulte que $ E$ a comme équation $ 4X'^2+2Y'^2-32=0$, soit encore

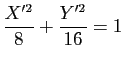
    $\displaystyle \dfrac{X'^2}{8}+\dfrac{Y'^2}{16}=1$

    dans ce nouveau repère.

  7. Le demi-grand axe de $ E$ vaut donc $ a=4$ et le demi-petit axe $ b=2\sqrt{2}$. La demi-distance focale $ c$ est définie par $ c^2=a^2-b^2$, d'où $ c=2\sqrt{2}$. L'excentricité de $ E$ est donnée par $ e=c/a=\sqrt{2}/2$. Le grand axe de $ E$ est porté par la droite d'équation $ x+y-5=0$ (axe $ \Omega Y'$ du nouveau repère) et le petit axe par la droite d'équation $ x-y+3=0$ (axe $ \Omega X'$ du nouveau repère) dans le repère $ (O,\vec{i},\vec{j})$.

  8. L'hyperbole $ H$ et l'ellipse $ E$ ont même centre, même axe focal, et même distance focale. Il en résulte qu'elles ont les mêmes foyers.

    \includegraphics[width=0.8\textwidth]{devoir}


Section : Entraînement
Avant : Devoir
Après : Compléments


         © UJF Grenoble, 2011                              Mentions légales