-
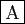
- L'axe
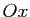 est axe de symétrie de
est axe de symétrie de 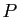 .
.
-
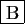
- Le foyer de
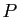 a pour coordonnées
a pour coordonnées
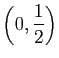 .
.
-
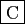
- La directrice de
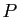 a pour équation
a pour équation
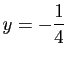 .
.
-
- La directrice de
 a pour équation
a pour équation
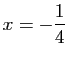 .
.
-
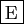
- Le foyer de
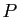 a pour coordonnées
a pour coordonnées
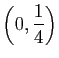 .
.
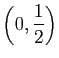 .
.
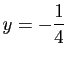 .
.
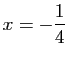 .
.
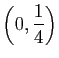 .
.
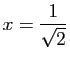 est une directrice de
est une directrice de
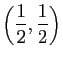 et
et
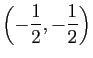 .
.
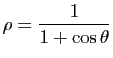 ;
;
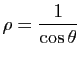 ;
;
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales