Exercice 1
Le plan est rapporté à un repère orthonormé. Écrire l'équation de la parabole 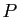 de foyer
de foyer 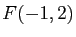 et de directrice
et de directrice 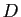 d'équation
d'équation 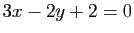 .
.
Exercice 2
Le plan est rapporté à un repère orthonormé. Écrire l'équation de l'ellipse 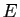 de foyer
de foyer 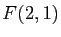 , de directrice
, de directrice 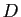 d'équation
d'équation 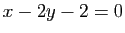 et d'excentricité
et d'excentricité
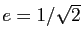 .
.
Exercice 3
Le plan est rapporté à un repère orthonormé. Écrire l'équation de l'ellipse 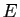 de foyers
de foyers 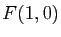 et
et 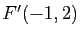 et de demi-grand axe de longueur 3.
et de demi-grand axe de longueur 3.
Exercice 4
Déterminer l'ensemble des centres des cercles passant par un point fixe 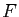 et tangents à un cercle fixe
et tangents à un cercle fixe 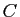 (on discutera selon la position de
(on discutera selon la position de 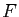 par rapport à
par rapport à 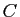 ).
).
Exercice 5
Montrer que deux coniques sont semblables si et seulement si elles ont la même excentricité.
Exercice 6
Montrer que deux paraboles sont isométriques si et seulement si elles ont le même paramètre.
Exercice 7
Intersection d'une parabole et d'une droite
- Montrer que toute parallèle à l'axe d'une parabole coupe celle-ci en exactement un point.
- Montrer que toute droite non parallèle à l'axe d'une parabole coupe celle-ci en 0, 1 ou 2 points. Montrer qu'elle coupe la parabole en exactement un point si et seulement si elle est tangente à la parabole.
Exercice 11
Soit 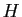 une hyperbole de demi-distance focale
une hyperbole de demi-distance focale 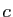 . Montrer qu'il existe un repère normé porté par les asymptotes de
. Montrer qu'il existe un repère normé porté par les asymptotes de 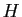 tel que l'équation de
tel que l'équation de 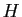 dans ce repère soit
dans ce repère soit
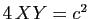 .
.
Exercice 12
Le plan affine euclidien est rapporté à un repère orthonormal. Soient 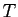 de coordonnées
de coordonnées
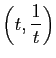 ,
,  de coordonnées
de coordonnées
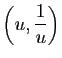 ,
, 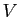 de coordonnées
de coordonnées
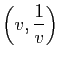 trois points distincts de l'hyperbole équilatère
trois points distincts de l'hyperbole équilatère 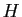 d'équation
d'équation 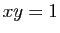 .
.
- Écrire l'équation de la perpendiculaire
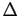 à la droite
à la droite 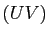 passant par
passant par 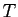 .
.
- Déterminer les coordonnées du second point d'intersection de
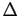 avec
avec 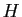 .
.
- Montrer que ce point appartient aux deux autres hauteurs du triangle
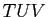 .
.
- En déduire que l'orthocentre de tout triangle dont les sommets appartiennent à une hyperbole équilatère appartient à cette même hyperbole.
Exercice 13
Soit, dans le plan rapporté à un repère orthonormal, 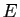 l'ellipse d'équation
l'ellipse d'équation
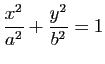 .
.
- Montrer qu'une droite est tangente à
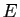 si et seulement si elle coupe
si et seulement si elle coupe 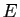 en un point et un seul.
en un point et un seul.
- Soit
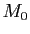 un point de coordonnées
un point de coordonnées 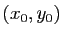 et
et 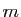 un réel. Donner une condition nécessaire et suffisante pour que la droite de pente
un réel. Donner une condition nécessaire et suffisante pour que la droite de pente 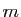 passant par
passant par 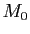 soit tangente à
soit tangente à 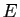 .
.
- Déterminer en fonction de
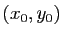 le nombre de tangentes à
le nombre de tangentes à 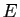 passant par
passant par 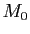 .
.
- Montrer que deux droites de pentes respectives
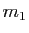 et
et 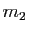 sont perpendiculaires si et seulement si
sont perpendiculaires si et seulement si 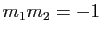 .
.
- Montrer que l'ensemble des points du plan d'où l'on peut mener deux tangentes à
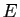 perpendiculaires entre elles
est un cercle de centre le centre de
perpendiculaires entre elles
est un cercle de centre le centre de 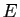 dont on précisera le rayon.
dont on précisera le rayon.
Exercice 15
Soit 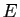 une ellipse de foyers
une ellipse de foyers 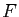 et
et 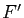 . Déterminer le lieu des images de
. Déterminer le lieu des images de 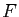 par :
par :
- les symétries orthogonales par rapport aux tangentes à
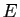 ;
;
- les projections orthogonales sur les tangentes à
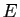 .
.
Exercice 16
Montrer que toute tangente à une hyperbole coupe les asymptotes de cette hyperbole en deux points distincts 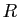 et
et 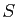 et que l'aire du triangle
et que l'aire du triangle 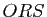 , où
, où 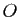 est le centre de l'hyperbole, ne dépend pas de la tangente considérée.
est le centre de l'hyperbole, ne dépend pas de la tangente considérée.
Exercice 18
Soit, dans le plan rapporté à un repère orthonormé
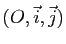 ,
, 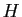 l'hyperbole équilatère d'équation
l'hyperbole équilatère d'équation 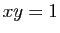 ,
, 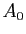 un point de
un point de 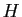 de coordonnées
de coordonnées 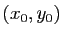 et
et 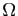 le symétrique de
le symétrique de 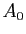 par rapport à
par rapport à 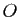 . Le cercle de centre
. Le cercle de centre 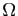 passant par
passant par 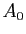 recoupe en général
recoupe en général 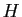 en trois points
en trois points 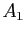 ,
, 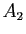 ,
, 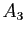 .
.
- Écrire une équation polynomiale de degré 3 vérifiée par les abscisses
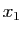 ,
, 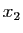 ,
, 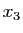 des points
des points 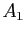 ,
, 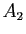 ,
, 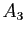 .
.
- En déduire, en utilisant les relations entre les coefficients et les racines d'un polynôme, que
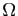 est l'isobarycentre du triangle
est l'isobarycentre du triangle 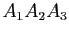 .
.
- Soit
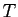 un triangle. On suppose que l'isobarycentre de
un triangle. On suppose que l'isobarycentre de 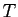 est aussi le centre du cercle circonscrit à
est aussi le centre du cercle circonscrit à 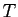 . Montrer que
. Montrer que 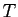 est équilatéral.
est équilatéral.
- Que peut-on dire du triangle
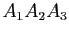 ?
?
Exercice 20
Montrer que l'image d'une ellipse ou d'un cercle par une application affine bijective est une ellipse ou un cercle.
Exercice 22
Soient 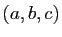 et
et
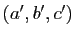 deux triplets de réels tels que
deux triplets de réels tels que
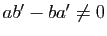 et
et 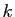 un réel non nul. Montrer que la courbe d'équation
un réel non nul. Montrer que la courbe d'équation
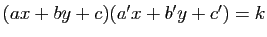 est une hyperbole dont on précisera le centre et les asymptotes.
est une hyperbole dont on précisera le centre et les asymptotes.
Exercice 23
Le plan est rapporté à un repère orthonormé. Montrer que la courbe d'équation
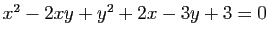 est une parabole. Déterminer les coordonnées de son foyer et l'équation de sa directrice.
est une parabole. Déterminer les coordonnées de son foyer et l'équation de sa directrice.
Exercice 24
Soit, dans le plan rapporté à un repère orthonormé, 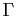 la conique d'équation
la conique d'équation
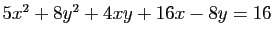 .
Réduire l'équation de
.
Réduire l'équation de 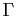 . On donnera les coordonnées du centre, les équations des axes, les longueurs du grand axe et du petit axe, les coordonnées des foyers.
. On donnera les coordonnées du centre, les équations des axes, les longueurs du grand axe et du petit axe, les coordonnées des foyers.
Exercice 26
Montrer que toute courbe de représentation paramétrique
où 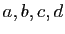 sont des réels, est une ellipse, un cercle ou un segment de droite de centre l'origine (on pourra, dans le cas où la courbe n'est pas portée par une droite, en écrire une équation cartésienne). Donner une condition nécessaire et suffisante pour que cette courbe soit un cercle (resp. un segment de droite).
sont des réels, est une ellipse, un cercle ou un segment de droite de centre l'origine (on pourra, dans le cas où la courbe n'est pas portée par une droite, en écrire une équation cartésienne). Donner une condition nécessaire et suffisante pour que cette courbe soit un cercle (resp. un segment de droite).
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
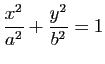 en :
en :
![\includegraphics[width=0.5\textwidth]{sousnormaleparabole}](img463.gif)
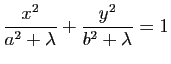
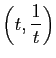 ,
, 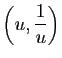 ,
, 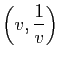 trois points distincts de l'hyperbole équilatère
trois points distincts de l'hyperbole équilatère 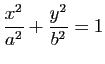 .
.
![]() une conique de foyer
une conique de foyer ![]() , de directrice
, de directrice ![]() et d'excentricité
et d'excentricité ![]() ,
, ![]() un point de
un point de ![]() ,
, ![]() son projeté orthogonal sur
son projeté orthogonal sur ![]() . On suppose que la tangente à
. On suppose que la tangente à ![]() en
en ![]() coupe la directrice
coupe la directrice ![]() en un point
en un point ![]() .
.
![\includegraphics[width=0.4\textwidth]{tangenteconique}](img486.gif)
![]() une hyperbole,
une hyperbole, ![]() son centre et
son centre et ![]() une droite passant par
une droite passant par ![]() et distincte des asymptotes de
et distincte des asymptotes de ![]() .
.
![]() ,
, ![]() l'ellipse de représentation paramétrique
l'ellipse de représentation paramétrique ![]() ,
, ![]() .
.
![\includegraphics[width=0.7\textwidth]{steiner}](img507.gif)
![]() un triangle non aplati et
un triangle non aplati et ![]() son centre de gravité. Montrer qu'il existe une ellipse tangente aux trois côtés de ce triangle en leurs milieux et passant par les milieux des segments
son centre de gravité. Montrer qu'il existe une ellipse tangente aux trois côtés de ce triangle en leurs milieux et passant par les milieux des segments ![]() ,
, ![]() et
et ![]() . (Indication : on se ramènera par une transformation affine au cas où le triangle est équilatéral.)
. (Indication : on se ramènera par une transformation affine au cas où le triangle est équilatéral.)
![]() .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales