Vrai-Faux 5
Parmi les affirmations
suivantes, lesquelles sont vraies, lesquelles sont fausses, et
pourquoi ?
-
 Si deux ellipses ont les mêmes foyers, l'une des deux est incluse dans l'intérieur de l'autre.
Si deux ellipses ont les mêmes foyers, l'une des deux est incluse dans l'intérieur de l'autre.
 Si une ellipse et une hyperbole ont les mêmes foyers, elles ne se coupent pas.
Si une ellipse et une hyperbole ont les mêmes foyers, elles ne se coupent pas.
 Deux ellipses distinctes se coupent en au plus deux points.
Deux ellipses distinctes se coupent en au plus deux points.
-
 Si deux ellipses distinctes ont en commun un foyer et la directrice associée, elles ne se coupent pas.
Si deux ellipses distinctes ont en commun un foyer et la directrice associée, elles ne se coupent pas.
-
 Si deux ellipses ont les mêmes foyers, elles ont le même centre.
Si deux ellipses ont les mêmes foyers, elles ont le même centre.
 Si deux ellipses ont en commun un foyer et la directrice associée, elles ont même centre.
Si deux ellipses ont en commun un foyer et la directrice associée, elles ont même centre.
-
 Si une ellipse et une hyperbole ont en commun un foyer et la directrice associée, elles ne se coupent pas.
Si une ellipse et une hyperbole ont en commun un foyer et la directrice associée, elles ne se coupent pas.
-
 Si une droite coupe une ellipse en exactement un point, elle est tangente à l'ellipse en ce point.
Si une droite coupe une ellipse en exactement un point, elle est tangente à l'ellipse en ce point.
-
 Une droite coupe une hyperbole en au plus deux points.
Une droite coupe une hyperbole en au plus deux points.
 Si une droite coupe une hyperbole en un point exactement, elle est tangente à l'hyperbole en ce point.
Si une droite coupe une hyperbole en un point exactement, elle est tangente à l'hyperbole en ce point.
 La tangente en
La tangente en 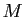 à
à 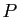 est la médiatrice de
est la médiatrice de ![$ [HF]$](img193.gif) .
.
 La normale à
La normale à 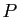 en
en 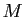 passe par
passe par 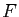 .
.
 Le milieu du segment
Le milieu du segment ![$ [HF]$](img193.gif) appartient à la tangente au sommet de
appartient à la tangente au sommet de 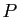 .
.
 La normale en
La normale en 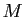 à
à 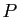 est parallèle à la droite
est parallèle à la droite 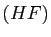 .
.
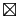 Toute droite perpendiculaire à
Toute droite perpendiculaire à 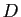 rencontre
rencontre 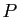 en un point et un seul.
en un point et un seul.
 Le symétrique de
Le symétrique de 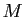 par rapport à
par rapport à 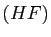 appartient à la tangente au sommet de
appartient à la tangente au sommet de 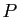 .
.
 Le symétrique de
Le symétrique de 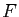 par rapport à toute tangente à
par rapport à toute tangente à 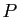 appartient à
appartient à 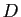 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales