Soient 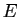 et
et 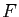 deux espaces vectoriels de dimension finie,
munis respectivement des bases
deux espaces vectoriels de dimension finie,
munis respectivement des bases
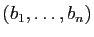 et
et
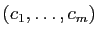 .
.
Une application linéaire 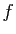 est
déterminée par les images des vecteurs
est
déterminée par les images des vecteurs
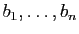 . Ces images
sont des combinaisons linéaires
. Ces images
sont des combinaisons linéaires
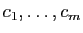 : pour tout
: pour tout
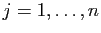 ,
,
Les
coordonnées 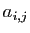 de ces vecteurs dans la base
de ces vecteurs dans la base
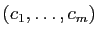 ,
rangés en
,
rangés en 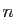 colonnes, forment la matrice de l'application
colonnes, forment la matrice de l'application 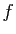 ,
relative aux bases considérées.
,
relative aux bases considérées.
Les opérations sur les applications linéaires se traduisent
en des opérations analogues sur les matrices.
Soient 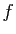 ,
, 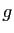 deux applications linéaires de
deux applications linéaires de 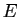 dans
dans 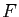 et
et 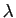 ,
, 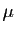 deux réels. Si les matrices de
deux réels. Si les matrices de 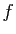 et
et 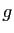 (relatives aux mêmes bases au départ et à l'arrivée) sont
(relatives aux mêmes bases au départ et à l'arrivée) sont  et
et 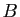 , alors la matrice de
, alors la matrice de
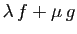 est
est
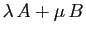 . La composée de deux applications linéaires
est encore une application linéaire.
Sa matrice est le produit des matrices de
. La composée de deux applications linéaires
est encore une application linéaire.
Sa matrice est le produit des matrices de
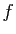 et
et 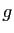 .
.
Remarquez que l'ordre dans lequel s'effectue le produit est l'ordre dans
lequel s'écrit la composition.
matrice de
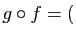
matrice de
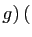
matrice de
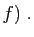
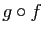 des vecteurs
des vecteurs
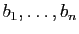 se calcule en
prenant l'image par
se calcule en
prenant l'image par 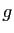 des vecteurs
des vecteurs
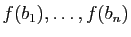 . On
calcule les coordonnées de ces images dans la base
. On
calcule les coordonnées de ces images dans la base
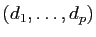 en effectuant le produit par la matrice de
en effectuant le produit par la matrice de 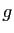 ,
des vecteurs exprimant
,
des vecteurs exprimant
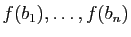 dans la base
dans la base
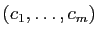 , qui sont les vecteurs colonnes de
, qui sont les vecteurs colonnes de  . Effectuer
successivement le produit de
. Effectuer
successivement le produit de 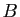 par chacun des vecteurs colonnes de
par chacun des vecteurs colonnes de
 revient à calculer le produit de
revient à calculer le produit de 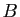 par
par  .
. 
Pour les endomorphismes (les espaces de départ et d'arrivée sont les
mêmes), nous conviendrons toujours de choisir la même base au
départ et à l'arrivée.
Proposition 5
Soit 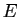 un espace vectoriel, muni de la base
un espace vectoriel, muni de la base
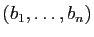 , et
, et
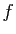 une application linéaire de
une application linéaire de 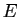 dans lui-même. L'application
dans lui-même. L'application
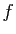 est un automorphisme si et seulement si la matrice de
est un automorphisme si et seulement si la matrice de 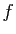 dans la
base
dans la
base
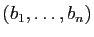 est inversible. Si c'est le cas, la matrice
de
est inversible. Si c'est le cas, la matrice
de 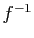 est l'inverse de la matrice de
est l'inverse de la matrice de 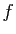 .
.
Démonstration : Observons d'abord que la matrice de l'application identique est la
matrice identité, quelle que soit la base. Si l'application 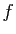 est
bijective, alors sa réciproque
est
bijective, alors sa réciproque 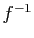 est l'unique application dont la
composée avec
est l'unique application dont la
composée avec 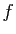 est l'application identique.
est l'application identique.
Si  est la matrice de
est la matrice de 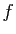 et
et 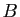 la matrice de
la matrice de 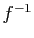 , la proposition
4
entraîne que
, la proposition
4
entraîne que
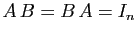 .
.
Réciproquement si  est
inversible, alors
est
inversible, alors 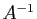 définit une application linéaire unique
de
définit une application linéaire unique
de 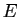 dans
dans 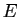 . La composée de cette application avec
. La composée de cette application avec 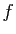 a pour
matrice
a pour
matrice 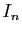 : c'est l'application identique. Donc cette application
est la réciproque de
: c'est l'application identique. Donc cette application
est la réciproque de 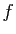 .
. 
Un automorphisme de 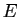 est une application linéaire qui envoie une
base de
est une application linéaire qui envoie une
base de 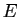 sur une autre base.
Effectuer un changement de base (remplacer une base par une autre)
revient à prendre l'image par l'automorphisme qui envoie la nouvelle
base sur l'ancienne, donc le produit par la matrice de cet
automorphisme.
sur une autre base.
Effectuer un changement de base (remplacer une base par une autre)
revient à prendre l'image par l'automorphisme qui envoie la nouvelle
base sur l'ancienne, donc le produit par la matrice de cet
automorphisme.
Démonstration : Notons 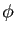 l'automorphisme de
l'automorphisme de 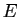 qui à
qui à 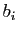 associe
associe 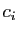 , pour
tout
, pour
tout
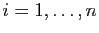 . Ecrivons :
. Ecrivons :
Par définition, les coordonnées de 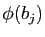 dans la base
dans la base
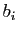 forment la
forment la 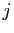 -ième colonne de la matrice
-ième colonne de la matrice
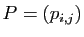 . Donc :
. Donc :
Comme les coordonnées dans la base
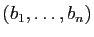 sont
uniques, on en déduit, pour tout
sont
uniques, on en déduit, pour tout
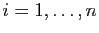 :
:
donc
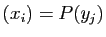 , d'où le résultat en multipliant à
gauche par
, d'où le résultat en multipliant à
gauche par 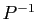 .
.
La matrice 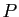 s'appelle la matrice de passage. Dans un changement de
base, nous conviendrons toujours de noter
s'appelle la matrice de passage. Dans un changement de
base, nous conviendrons toujours de noter 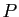 la matrice qui donne les
nouveaux vecteurs en fonction des anciens. Voici un exemple. Munissons
la matrice qui donne les
nouveaux vecteurs en fonction des anciens. Voici un exemple. Munissons
 , des deux bases suivantes.
, des deux bases suivantes.
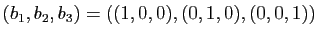
et
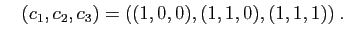
Voici la matrice de passage 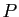 et son inverse.
et son inverse.
Si un vecteur 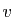 a pour coordonnées
a pour coordonnées 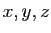 dans la base canonique
dans la base canonique
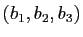 , alors ses coordonnées dans la base
, alors ses coordonnées dans la base
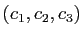 s'obtiennent en effectuant le produit :
s'obtiennent en effectuant le produit :
Constatez que :
On peut appliquer ce qui précède pour trouver la matrice d'un
endomorphisme quelconque dans la nouvelle base : c'est
la formule de changement de base.
Démonstration : Notons 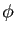 l'application qui à
l'application qui à 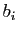 associe
associe 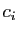 .
La matrice de
.
La matrice de 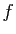 dans la base
dans la base
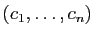 a pour vecteurs
colonnes les images des vecteurs
a pour vecteurs
colonnes les images des vecteurs
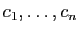 . Pour calculer
. Pour calculer
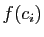 , on peut calculer
, on peut calculer
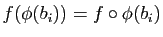 . Donc les coordonnées des vecteurs
. Donc les coordonnées des vecteurs
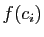 dans la base
dans la base
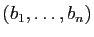 sont les colonnes de la
matrice de
sont les colonnes de la
matrice de
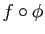 , qui est
, qui est 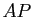 . D'après la proposition
6, pour obtenir les coordonnées
de ces vecteurs dans la base
. D'après la proposition
6, pour obtenir les coordonnées
de ces vecteurs dans la base
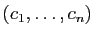 , il faut multiplier
à gauche par la matrice
, il faut multiplier
à gauche par la matrice 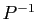 , d'où le résultat.
, d'où le résultat.
Reprenons l'exemple en dimension 3 des deux bases :
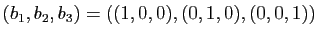
et
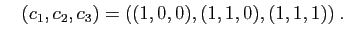
Considérons l'application de
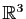 dans
dans
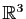 définie par :
définie par :
Sa matrice dans la base canonique
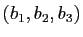 est :
est :
La matrice de 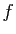 dans la base
dans la base
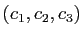 est :
est :
L'image par 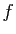 du vecteur
du vecteur
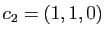 est le vecteur
est le vecteur
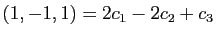 . Les coordonnées
. Les coordonnées 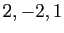 figurent dans
la seconde colonne de
figurent dans
la seconde colonne de 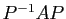 .
.
Le théorème 2 affirme que deux matrices
sont semblables si et seulement si elles représentent le même
endomorphisme dans des bases différentes. Il se généralise à
des applications linéaires quelconques,
comme suit.
La démonstration est pratiquement la même que celle du théorème
2, avec des notations plus lourdes. Nous
l'omettons.
Le théorème 3 affirme que deux matrices
sont équivalentes si et seulement si elles peuvent représenter la
même application linéaire,
à un changement de base près dans les espaces de
départ et d'arrivée.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() et
et ![]() deux espaces vectoriels de dimension finie,
munis respectivement des bases
deux espaces vectoriels de dimension finie,
munis respectivement des bases
![]() et
et
![]() .
.
![]() est
déterminée par les images des vecteurs
est
déterminée par les images des vecteurs
![]() . Ces images
sont des combinaisons linéaires
. Ces images
sont des combinaisons linéaires
![]() : pour tout
: pour tout
![]() ,
,
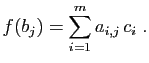
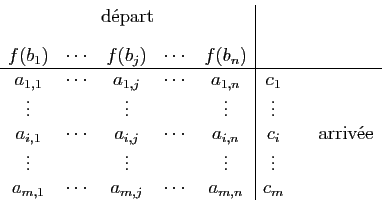
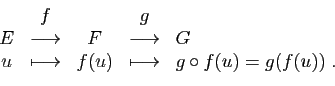
![]() est
inversible, alors
est
inversible, alors ![]() définit une application linéaire unique
de
définit une application linéaire unique
de ![]() dans
dans ![]() . La composée de cette application avec
. La composée de cette application avec ![]() a pour
matrice
a pour
matrice ![]() : c'est l'application identique. Donc cette application
est la réciproque de
: c'est l'application identique. Donc cette application
est la réciproque de ![]() .
. ![]()
![]() est une application linéaire qui envoie une
base de
est une application linéaire qui envoie une
base de ![]() sur une autre base.
Effectuer un changement de base (remplacer une base par une autre)
revient à prendre l'image par l'automorphisme qui envoie la nouvelle
base sur l'ancienne, donc le produit par la matrice de cet
automorphisme.
sur une autre base.
Effectuer un changement de base (remplacer une base par une autre)
revient à prendre l'image par l'automorphisme qui envoie la nouvelle
base sur l'ancienne, donc le produit par la matrice de cet
automorphisme.
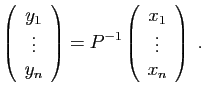
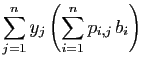
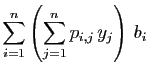
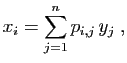
![]() s'appelle la matrice de passage. Dans un changement de
base, nous conviendrons toujours de noter
s'appelle la matrice de passage. Dans un changement de
base, nous conviendrons toujours de noter ![]() la matrice qui donne les
nouveaux vecteurs en fonction des anciens. Voici un exemple. Munissons
la matrice qui donne les
nouveaux vecteurs en fonction des anciens. Voici un exemple. Munissons
![]() , des deux bases suivantes.
, des deux bases suivantes.
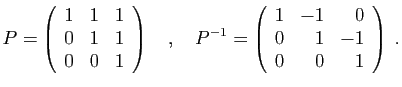
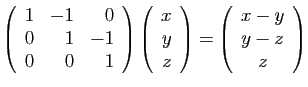
![]() dans la base
dans la base
![]() est
est
![]() .
.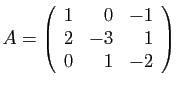
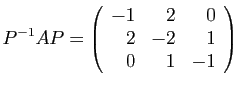
![]() relative aux bases
relative aux bases
![]() et
et
![]() est
est
![]() .
. © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales