En général si le produit 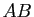 est défini, le produit
est défini, le produit 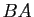 n'a
aucune raison de l'être. Le produit d'une matrice par sa
transposée est une exception, les
matrices carrées en sont une autre : si
n'a
aucune raison de l'être. Le produit d'une matrice par sa
transposée est une exception, les
matrices carrées en sont une autre : si  et
et 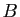 sont deux
matrices à
sont deux
matrices à 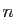 lignes et
lignes et 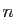 colonnes, les produits
colonnes, les produits 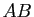 et
et 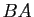 sont tous deux définis et ils ont les mêmes dimensions que
sont tous deux définis et ils ont les mêmes dimensions que  et
et
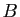 . En général ils ne sont pas égaux. Par exemple,
. En général ils ne sont pas égaux. Par exemple,
Nous noterons simplement
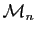 l'ensemble
l'ensemble
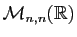 des matrices carrées à
des matrices carrées à 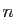 lignes et
lignes et 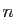 colonnes, à
coefficients réels. Parmi elles la matrice identité,
notée
colonnes, à
coefficients réels. Parmi elles la matrice identité,
notée 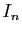 joue un rôle particulier.
joue un rôle particulier.
En effet, elle est l'élément neutre du produit matriciel :
pour toute matrice
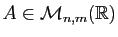 ,
,
On le vérifie facilement à partir de la définition
1.
Par exemple :
Nous verrons plus loin une méthode qui permet de savoir si
une matrice est inversible, et de calculer son inverse quand elle
l'est.
Observons que l'inverse, s'il existe, est nécessairement
unique. En effet, soient 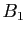 et
et 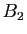 deux matrices telles que
deux matrices telles que
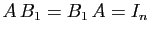 et
et
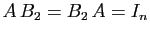 .
En utilisant l'associativité,
le produit
.
En utilisant l'associativité,
le produit
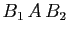 vaut
vaut
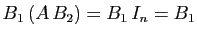 ,
mais aussi
,
mais aussi
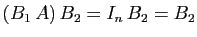 . Donc
. Donc 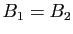 .
.
Il suffit de trouver une matrice 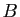 telle
que
telle
que 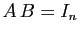 pour être sûr que
pour être sûr que  est
inversible et que son inverse est
est
inversible et que son inverse est 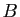 .
.
Théorème 1
Soit  une matrice de
une matrice de
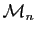 . Supposons qu'il existe une
matrice
. Supposons qu'il existe une
matrice 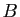 telle que
telle que 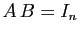 ou bien
ou bien 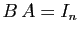 . Alors
. Alors  est
inversible et
est
inversible et 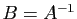 .
.
Démonstration : Supposons qu'il existe une matrice 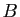 telle que
telle que 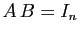 .
Considérons l'application, de
.
Considérons l'application, de
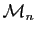 dans lui-même, qui à
une matrice
dans lui-même, qui à
une matrice 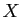 associe le produit
associe le produit 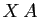 . D'après le point 3
de la proposition 1, c'est une application
linéaire, donc un endomorphisme de l'espace vectoriel
. D'après le point 3
de la proposition 1, c'est une application
linéaire, donc un endomorphisme de l'espace vectoriel
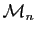 .
Montrons qu'elle est injective, c'est-à-dire que son noyau ne
contient que la matrice nulle. Si
.
Montrons qu'elle est injective, c'est-à-dire que son noyau ne
contient que la matrice nulle. Si 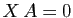 , alors
, alors
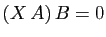 , mais
, mais
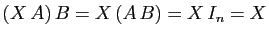 par hypothèse : donc
par hypothèse : donc 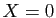 .
Une application linéaire
entre deux espaces de même dimension qui est injective est aussi
surjective. Donc il existe une matrice
.
Une application linéaire
entre deux espaces de même dimension qui est injective est aussi
surjective. Donc il existe une matrice
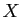 telle que
telle que 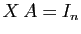 . Il reste à vérifier que cette matrice
est
. Il reste à vérifier que cette matrice
est 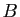 . Si
. Si
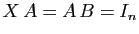 , alors
, alors
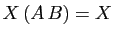 et
et
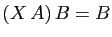 . D'où le résultat.
. D'où le résultat.
On procède de façon symétrique si 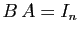 , en considérant
l'application qui à
, en considérant
l'application qui à 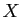 associe
associe 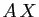 .
.
Si  et
et 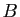 sont deux matrices inversibles de
sont deux matrices inversibles de
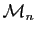 , leur
produit est inversible.
, leur
produit est inversible.
Proposition 3
Soient  et
et 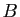 deux matrices inversibles de
deux matrices inversibles de
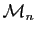 . Le
produit
. Le
produit 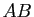 est inversible et son inverse est
est inversible et son inverse est
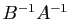 .
.
Démonstration : Nous utilisons le théorème 1, ainsi que
l'associativité du produit :

 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
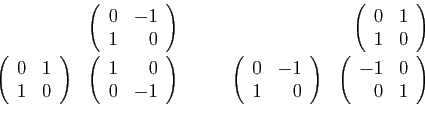

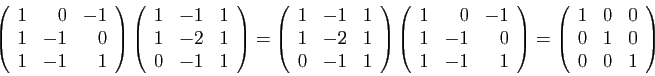
![]() telle
que
telle
que ![]() pour être sûr que
pour être sûr que ![]() est
inversible et que son inverse est
est
inversible et que son inverse est ![]() .
.
![]() , en considérant
l'application qui à
, en considérant
l'application qui à ![]() associe
associe ![]() .
.![]()
![]() et
et ![]() sont deux matrices inversibles de
sont deux matrices inversibles de
![]() , leur
produit est inversible.
, leur
produit est inversible.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales